Dado el triángulo ABC trazar una paralela a AB tal que divida el perímetro por la mitad.

Barroso, R. (2004): Comunicación personal.

Solución de José María Gavilán Izquierdo, profesor de Didáctica de las Matemáticas y Matemáticas (Depto. Didáctica de las Matemáticas) en la Universidad de Sevilla.

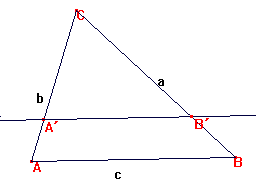
Consideramos una homotecia de centro C y razón k, con 0<k<1. Quedando la figura siguiente:

Los triángulos ABC y A´B´C son semejantes de razón k. Por tanto las longitudes de sus lados son proporcionales con coeficiente de proporcionalidad k.

Como queremos que la recta divida el perímetro de ABC por la mitad, tenemos que ka+kb= (a+b+c)/2, tomando la constante k como (a+b+c)/2(a+b) tenemos lo que se pide.

Además a+b+c>a+b luego (a+b+c)/(a+b)>1 luego (a+b+c)/2(a+b)>1/2 se garantiza la existencia en el iinterior de ABC del triángulo planteado en el problema 190:

Problema 190

Dado el triángulo ABC se traza una paralela a AB

tal que divida el perímetro por la mitad.

Se traza otras paralelas a BC y CA con la misma

condición. Estas tres paralelas conforman el triángulo MNP

También como k<1, a+b+c<2(a+b), para que tenga "sentido" la figura y la recta paralela esté en el interior de ABC.

La construcción es construyendo la homotecia de centro C y razón (a+b+c)/2(a+b). [La construcción del cociente de dos segmentos con regla y compás puede verse en La geometría de Descartes].

Dado ABC llevemos c sobre la semirrecta de origen C que pasa por A con una circunferencia de centro A y radio c.

Construyamos a partir de b+c el perímetro b+c+a, transportando a por paralelas y con otra circunferencia.

Sobre la semirrecta de origen C que pasa por B por paralelas y mediante circunferencia construyamos a+b.

Con otra circunferencia construyamos 2(a+b).

Construyamos el triángulo correspondiente de lados perímetro sobre CA y 2/(a+b) sobre CB.

Por B tracemos una paralela a la base del construido, que nos dará sobre CA ka.

Llevemos con una circunferencia ka sobre CB, y tendremos B'. Una paralela a AB sobre B' nos dará la solución CA'B'..