PROBLEMA DE MALFATTI.
Notas sobre este problema clásico de F. Damián Aranda Ballesteros, profesor
del IES Blas Infante, de Córdoba.
DADO UN TRIÁNGULO, CONSTRUIR TRES CIRCUNFERENCIAS,
TANGENTES DOS A DOS ENTRE SÍ Y A SU VEZ A CADA PAR DE LADOS DEL TRIÁNGULO.

Este problema fue propuesto por el matemático italiano
Malfatti (1731-1807) en 1803 y resuelto de manera algebraica
y en el Volumen nº 50 de
Presentaremos dos soluciones, la
primera expuesta en el volumen 45 de The Crelle's Journal debida a
Schellbach y la segunda, más geométrica debida a Jakob Steiner aunque la
demostración de la misma sea de Hart.
PRIMERA CONSTRUCCIÓN DE MALFATTI (SCHELLBACH)
Sean las circunferencias de Malfatti que deseamos
obtener, de radios m, n, y p, siendo los segmentos de las tangencias con los
lados del triángulo t, v, w.
Sea ABC el triángulo, de
lados a,b,c; el perímetro 2×s = a+b+c y los ángulos a,b, g.
Sean las circunferencias de Malfatti
que deseamos obtener, de radios m, n, p
y los segmentos de las tangencias con los lados del triángulo t, v, w. 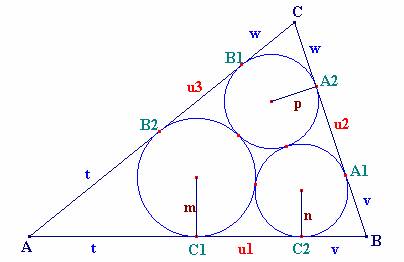
Hagamos una serie de
consideraciones sobre la circunferencia inscrita en el triángulo ABC. Si
llamamos r al radio de esta circunferencia, y A’, B’, C’ a los puntos de
contacto con los lados del triángulo, sean además a1
, b1 , c1 , los segmentos de tangencia desde los
ángulos en A, B y C, respectivamente.
 De las tres igualdades:
De las tres igualdades:
b1 + c1 = a; c1
+ a1 = b; a1 +b1 = c; se sigue que: a1 = s-a, b1 = s-b, c1 = s-c.
Por otro lado, como los puntos I y O1 pertenecen a la bisectriz del
ángulo en A, tenemos que:
![]() , de donde m=
, de donde m=![]() . De igual modo, obtenemos
n=
. De igual modo, obtenemos
n= ![]() ; p=
; p= ![]() .
.
De las relaciones entre los segmentos u1 y los radios m, n deducimos
que:
u12 = (m+n)2 -(m-n)2 ; u1
= 2 y de forma
similar: u2 = 2; u3 =2.
Sustituyendo
las relaciones antes encontradas para m, n y p, obtenemos:
u1 = 2= 2.![]() ;
;
u2 = 2= 2.![]()
![]() ;
;
u3 = 2![]() = 2.
= 2.![]()
![]()
De la expresión del área del triángulo S= r×s = =![]() ® r2×s= a1×b1×c1 ® r2 =
® r2×s= a1×b1×c1 ® r2 =![]() . Esta expresión simplifica las de u1
, u2 , u3 del siguiente modo:
. Esta expresión simplifica las de u1
, u2 , u3 del siguiente modo:
u1 = 2.![]() ; u2
= 2.
; u2
= 2.![]()
![]() ; u3
= 2.
; u3
= 2.![]()
![]()
Así, los lados del triángulo se pueden expresar del siguiente modo:
a= v + u2 + w = v +2.![]()
![]() + w;
+ w;
b= w + u3 + t = w +2.![]()
![]() + t;
+ t;
c= t + u1 + v = t +2.![]() + v; Tomando s,
semiperímetro del triángulo ABC, como unidad de longitud, podemos simplificar
las anteriores igualdades del siguiente modo:
+ v; Tomando s,
semiperímetro del triángulo ABC, como unidad de longitud, podemos simplificar
las anteriores igualdades del siguiente modo:
a= v +2.![]()
![]() + w;
+ w;
b= w+2.![]()
![]() + t;
+ t;
c= t +2. ![]() + v;
+ v;
Ahora consideramos a, b, c, v, w, t como los cuadrados de los senos de seis
ángulos agudos a, b, g, f, w, t. Esto es:
sen2 a= a; sen2 b= b; sen2 g = c; sen2 f = v; sen2 w= w; sen2 t = t. Según estas
igualdades, también se puede sustituir a1 ,
b1 y c1 , ya que:
a + a1 = s=1 ; Luego: sen2 a + a1 = 1® a1 = cos2 a .
De
igual modo b1 = cos2 a ; c1 = cos2
g y así podemos expresar las anteriores
igualdades de la forma siguiente:
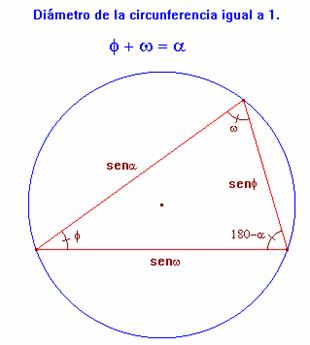
sen2
a = sen2 f +sen2 w+2×sen f×sen w× cos a
sen2 b = sen2 w +sen2 t+2× sen w×sen t× cos b
sen2 g = sen2 t + sen2 f +2× sen t×sen f× cos g
Observemos cualquiera de estas ecuaciones.
Sea
por ejemplo la primera de ellas; trata de la relación trigonométrica conocida
que existe entre los lados de un triángulo inscrito en una circunferencia de
diámetro la unidad, dos de cuyos ángulos
son f, w,
relacionados tal que:
Utilizando
el teorema del coseno para este triángulo, obtenemos que:
sen2 a = sen2 f + sen2 w + 2×
sen f×sen
w× cos a.
|
|
Por
tanto, de las anteriores igualdades, se seguirá que son equivalentes a las
siguientes:
f + w = a; w + t = b; f + t = g
Si
las sumamos todas y llamamos s = (a+b+g) / 2 ,
entonces f + w+
t = s, y obtendremos las
siguientes ángulos:
t = s - a ;
f = s- b ;
w = s- g .
De
aquí se deriva la siguiente
Construcción:
1.- Determinar los
tres ángulos agudos a, b, g , cuyos senos al cuadrado son iguales
respectivamente, a los lados a, b, c, del triángulo dado ABC.
2.- Obtenemos la semisuma de los ángulos anteriores, siendo s = (a+b+g) / 2, para así después hallar los tres nuevos
ángulos t = s
- a ;
f = s- b ; w
= s- g.
3.- Una vez hallados los ángulos anteriores t , f , w, se tratará de determinar los cuadrados de los senos de estos ángulos, es
decir, sen2 t =t, sen2
f =v, sen2 w =w , obteniendo de este modo los segmentos de las
tangentes orientadas a partir de los vértices del triángulo, concluyendo de
este modo.
Nota: Para construir el cuadrado del seno de un ángulo dado k, k = sen2 k, procederemos de la siguiente forma:
Dada la circunferencia de diámetro la unidad, HK =1, construyamos el ángulo k, sobre KH y con vértice en K, obteniendo así
el punto L, intersección del lado KL con
la circunferencia dada. Trazamos por L la perpendicular LM a HK, obteniendo así
el punto M, pie de esta perpendicular sobre HK.
El segmento HM es precisamente sen2 k = k
SEGUNDA CONSTRUCCIÓN DE MALFATTI (STEINER)
LEMA 1.
|
|
|
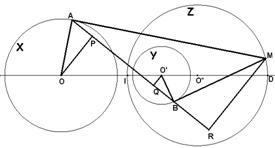
Si A y B son los puntos de contacto, en dos circunferencias X e Y, de
las tangentes trazadas desde un punto cualquiera M de su circunferencia de
similitud[1],
entonces la tangente de A hasta Y es igual a la tangente trazada de B hasta X.
Dem.-
En primer lugar, las circunferencias X, Y verifican con Z, su circunferencia de
similitud, que las tangentes trazadas desde cualquier punto de Z hasta X e Y
vienen dadas por una razón constante, en este caso, igual a la razón de sus
radios.
Esto
es consecuencia de que el L.G. de los puntos M, donde la razón de sus
distancias hasta los centros O y O' de dos circunferencias dadas es igual a la
razón de sus radios es su circunferencia de similitud.
Trazamos la recta AB y sobre ella proyectamos ortogonalmente los puntos O, O' y
M en P, Q y R. Este hecho propicia las semejanzas entre los siguientes
triángulos ARM y OPA por un lado y BRM y O'QB por otro.
De estas relaciones deducimos que
AP/MR=OA/AM y MR/QB= MB/O'B; entonces tenemos que (AP/MR)×(MR/QB)=(OA/AM)×(MB/O'B);
AP/QB=(OA/O'B)×(MB/AM)=1.
Por tanto, AP=QB, es decir, la secante AB determina dos cuerdas AA' y B'B
iguales en las circunferencias X e Y. Esto establece que la tangente de A hasta
Y es igual a la tangente trazada de B hasta X ya que AB'= BA' y, por tanto AT2=AB'×AB =BA'×BA = BT'2.
El
recíproco de este lema es igualmente válido.
LEMA 2.
Si dos tangentes comunes exteriores DB y DC, relativas a dos parejas distintas de circunferencias (a, c) y (a, b) y una tangente común interior DA relativa a la tercera pareja (b, c) concurren en un mismo punto D, entonces las otras tres tangentes EF, EC y EA, asociadas a las anteriores, concurren en un mismo punto E.
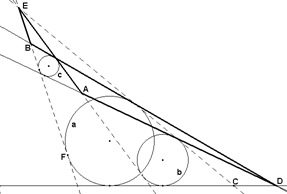
Sea E el
punto de intersección de EC, tangente exterior al par (a, b) y EA, tangente
interior al par (b, c). Por dicho punto trazamos EF, tangente exterior a la
circunferencia a. Veamos que, en efecto, esta recta EF también es tangente a la
circunferencia c. Para ello será suficiente demostrar que el cuadrilátero EADB
está circunscrito a la circunferencia c.
Por un lado, el cuadrilátero DCEB está
circunscrito al círculo a, y así tenemos que DC +CE = EB +BD; por otro lado, el
cuadrilátero DCEA está circunscrito al círculo b, y así tenemos que DC +CE = EA
+AD; luego entonces se verifica EB +BD = EA + AD. Como quiera que el lado EB
era tangente a la circunferencia a, ahora lo será también a la
circunferencia c y así, la tercera
tangente pasará por el punto E.
PROBLEMA
DE MALFATTI.
Sean
D, E, F los puntos de contacto entre sí de los tres círculos a trazar a, b, c.
Las rectas tangentes a ellas en D, E y F serán los ejes radicales de dichos
círculos tomados dos a dos; por tanto estas rectas concurrirán en el centro
radical L de a, b y c.
Sean
G y H los puntos del lado BC donde contactan las circunferencias b y c.
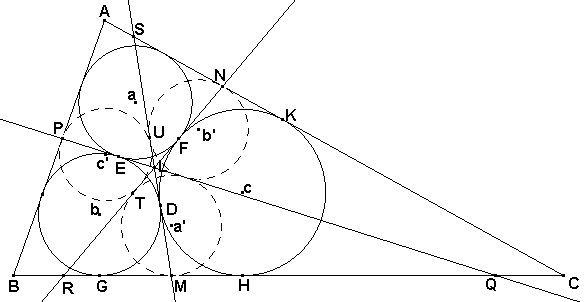
Como
MG =MD =MH y, por otro lado LE =LF entonces:
MQ -MR =GQ -RH =QE -RF =QL -RL; en definitiva MQ -MR =QL -RL, lo que significa que M es el punto donde el lado
RQ toca a la circunferencia inscrita al triángulo RLQ. Sea este círculo a'. De
manera análoga representamos por b' y c' los círculos que tocan respectivamente
a los lados AC y AB en los puntos N y P.
Consideramos ahora el sistema formado por los
círculos a', b', c. Tenemos las siguientes tangentes comunes: PQ, interior
común al par (a',b'); MS, exterior común al par (b',c)
y RN, exterior común al par (a', c).
Estas tangentes se cortan en el punto L y, por tanto por el Lema 2, las otras
tres tangentes asociadas serán también concurrentes. Como dos de ellas, AC y BC
concurren en C, necesariamente la tercera
tangente, que será la interior común al par (a', b') deberá pasar por C.
Ahora bien, de las relaciones MD =MH =TF; DU =KN
=FN, tenemos que
MU
=MD +DU =TF+FN =TN. Es decir, tenemos
que desde un punto M de a', la tangente trazada hasta b', MU, es igual a la
tangente trazada desde el punto N de b' hasta a', TN. Por tanto, por el
recíproco del lema1, las tangentes en M y N a los círculos a' y b' se cortan en
el punto C de su círculo de similitud. Por esta razón, los círculos a' y b' serán
vistos así desde C por el mismo ángulo. Este hecho significará que la segunda
tangente interior común a los círculos a' y b' será la bisectriz interior al
ángulo C.
Construcción: Sea I el centro del círculo inscrito al
triángulo ABC, inscribamos las circunferencias en cada uno de los triángulos
IAB, IBC y ICA. Trazamos las segundas tangentes comunes interiores de cada uno
de los pares de circunferencias; así se obtienen triángulos formados por dos de
los lados del triángulo y por tercer lado, cada una de las tangentes así
trazadas:
LOS CÍRCULOS INSCRITOS EN ESTOS TRIÁNGULOS SON LOS DE MALFATTI.
VARIACIONES SOBRE MALFATTI.
Podemos hacer algunas extensiones
sobre las anteriores construcciones. Una de ellas consistirá en reemplazar los
lados del triángulo por círculos tangentes entre sí.
La variación del problema pues,
será como sigue:
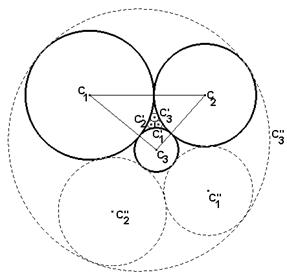
Dados tres círculos C1, C2, C3 tangentes entre
sí dos a dos, construir otros tres círculos C'
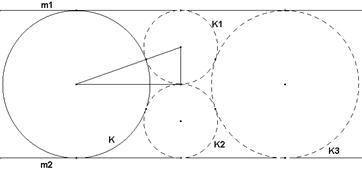 Este problema se puede resolver usando el
método general de Steiner. Sin embargo podemos elegir otro camino más sencillo,
el de la inversión. De este modo, si consideramos como centro de la inversión
el punto de contacto entre dos de las tres circunferencias dadas; sea por
ejemplo el punto de contacto entre C1 y C2. Así estos
círculos se transformarán en dos rectas paralelas m1 y m2
y la imagen del tercero, C3, será la de un círculo K, tangente a las
rectas m1 y m2. La forma de resolver el problema pasará
por la construcción de las circunferencias Ki, i=1,2,3
de la forma siguiente. Si la distancia entre m1 y m2 es
4r, entonces los radios de K1 y K2 serán ambos iguales a
r, mientras que los radios de K y K3 serán ambos iguales a 2r. La
distancia del centro de K a cada uno de los centros de las circunferencias K1
o K2 es igual a
Este problema se puede resolver usando el
método general de Steiner. Sin embargo podemos elegir otro camino más sencillo,
el de la inversión. De este modo, si consideramos como centro de la inversión
el punto de contacto entre dos de las tres circunferencias dadas; sea por
ejemplo el punto de contacto entre C1 y C2. Así estos
círculos se transformarán en dos rectas paralelas m1 y m2
y la imagen del tercero, C3, será la de un círculo K, tangente a las
rectas m1 y m2. La forma de resolver el problema pasará
por la construcción de las circunferencias Ki, i=1,2,3
de la forma siguiente. Si la distancia entre m1 y m2 es
4r, entonces los radios de K1 y K2 serán ambos iguales a
r, mientras que los radios de K y K3 serán ambos iguales a 2r. La
distancia del centro de K a cada uno de los centros de las circunferencias K1
o K2 es igual a ![]() . Este problema admite dos soluciones, dispuestas
simétricamente a un lado y otro de la circunferencia K, según que los contactos
sean exteriores o interiores. La imagen por la inversión de estas
circunferencias resolverá el problema.
. Este problema admite dos soluciones, dispuestas
simétricamente a un lado y otro de la circunferencia K, según que los contactos
sean exteriores o interiores. La imagen por la inversión de estas
circunferencias resolverá el problema.
Los siguientes dibujos ilustrarán los casos posibles.
|
|
|
CÍRCULOS DE MALFATTI PARA EL TRIÁNGULO EQUILÁTERO.
Problema.- Probar que para el triángulo equilátero,
las circunferencias de Malfatti no dan la solución a la siguiente cuestión:
" De un triángulo dado hay que cortar tres círculos interiores de manera
que la suma de sus áreas sea máxima"
BIBLIOGRAFÍA.
- BOTTEMA, O. The Malfatti Problem. Forum
Geometricorum. Vol I.
Págs. 43-50. 2001. - CASEY, J. A sequel to the First Six
Books of the Elements of Euclid, Ed. Hodges, Figgis & Co., 1888.
- DÖRRIE, Heinrich. 100 Great Problems of
Elementary Mathematics.
Dover Publications. 1965. - ROUCHÉ, E.
Traité de Géométrie. Ed. Gauthier-Villars. 1891.
- SHARIGUIN,
I. Problemas de Geometría.
Planimetría. Ed. Mir. 1986.