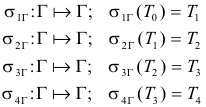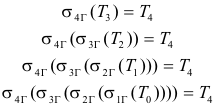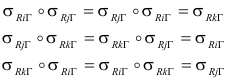GERGONNE Y EL PROBLEMA DE CASTILLON José María Pedret. Ingeniero Naval. Esplugues de Llobregat (Barcelona). |
||||
|
||||
En el problema número 82 del Laboratorio Virtual de triángulos con Cabri II de RICARDO BARROSO CAMPOS, se propuso y resolvió el PROBLEMA DE CASTILLON. Sobre la misma cuestión, Michel Chasles dice lo siguiente en su Aperçu historique sur l’origine et le développement des méthodes en géométrie, Nota XI.: “Sobre la cuestión de inscribir en un círculo un triángulo cuyos tres lados deben pasar por tres puntos dados. Pappus ha dejado una solución fácil de este problema para el caso en que los tres puntos están en línea recta. El caso general, que ofrece dificultad, fue propuesto en 1742 por Cramer a Castillon, que ya había dado muestras de habilidad en Geometría Antigua. Castillon halló una solución del problema, fundada en puras consideraciones de Geometría; la cual apareció en las Memorias de la Academia de Berlín de 1776.
Poco después, Lagrange da una solución diferente, puramente analítica y muy elegante. (Memorias de Berlín, 1776.) En 1780, Euler, N. Fuss y Lexell también resolvieron este problema (Memorias de la Academia de Petersburgo.) La solución de Euler da lugar a esta observación, que reposa sobre un lema que es precisamente el teorema de Stewart, del cual hemos hablado tratando el tema de los lemas de Pappus sobre el Tratado de lugares planos de Apolonio. (1ª Epoca, § 36.) Giordano di Oltaiano, joven napolitano, concibió la cuestión de una manera más general, y la resolvió para un polígono de un número cualquiera de lados, debiendo pasar por el mismo número de puntos colocados arbitrariamente en el plano del círculo. Malfati no tarda nada en resolverla en este estado de generalidad. (Las Memorias de estos dos geómetras están comprendidas en el tomo IV de las Memorias de la sociedad italiana.) Lhuillier aportó algunas modificaciones a las soluciones de estos dos geómetras, en las Memorias de Berlín de 1796; y vuelve sobre esta cuestión en sus Elementos de análisis geométrico y de análisis algebraico, año 1809. Carnot. En su Geometría de posición, retoma la solución de Lagrange, e hizo, introduciendo consideraciones geométricas, una solución mixta, que aplicó al caso general de un polígono cualquiera. Brianchon introdujo en esta cuestión un nuevo elemento de generalización; tomando una cónica cualquiera en lugar de un círculo; y la resolvió para el caso del triángulo, y suponiendo los tres puntos en línea recta. (Journal de l’école polytechnique, 10e cahier.) Gergonne dio un nuevo paso, tomando también una cónica, pero devolviendo a los tres puntos su generalidad de posición, y usando sólo la regla para resolver el problema. Las soluciones anteriores exigían el empleo del compás (Anales de Matemáticas, tomo I, página 341, años 1810-1811). Gergonne no había abordado directamente el problema: había propuesto otro que le era análogo; CIRCUNSCRIBIR, A UNA CÓNICA, UN TRIÁNGULO CUYOS VÉRTICES ESTÉN SOBRE TRES RECTAS DADAS. La construcción de este geómetra empleaba sólo la regla, y era un modelo de elegancia y simplicidad. Fue demostrada por Servois y Rochat (Anales de Matemáticas, tomo I, páginas 337 y 342). Gergonne observó que, por la teoría de polos en secciones cónicas, se transformaba inmediatamente en una solución de la misma naturaleza, para la cuestión de inscribir en una cónica un triángulo cuyos lados pasan por puntos dados. Quedaba, para completar esta materia, resolver también, para una sección cónica en lugar del círculo, el caso general de un polígono cualquiera. Es Poncelet a quien se debe este último esfuerzo. La solución de este geómetra coronaba dignamente los trabajos de sus antecesores. Ella ofrece, bajo todos los aspectos, un bello ejemplo de la perfección que pueden conseguir las teorías de la Geometría moderna. (Ver Tratado de las propiedades proyectivas, página 352.)” |
||||
|
||||
Resolvamos el problema abordado por Gergonne: CIRCUNSCRIBIR, A UNA CÓNICA, UN TRIÁNGULO CUYOS VÉRTICES ESTÉN SOBRE TRES RECTAS DADAS |
||||
|
||||
0. INTRODUCCION |
||||
|
||||
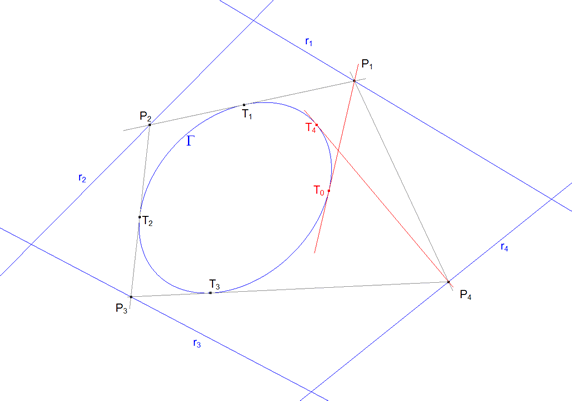 figura 1 figura 1
|
||||
Este es el caso particular, para n=3, del problema general de circunscribir a una cónica un polígono de n lados y cuyos n=vértices estén sobre n rectas. Nosotros desarrollaremos el método para un polígono de n=4 lados. Una vez deducido el método, lo aplicaremos al caso n=3 y estableceremos la solución.
Supongamos que tenemos la cónica Γ y n=4 rectas r1 ,r2 , r3, rn=4. Supongamos ahora que queremos resolver el problema tanteando. Tomamos P1 sobre r1 y trazamos las tangentes desde este punto a la cónica, obtenemos los puntos de contacto T0 y T1 sobre Γ y el punto P2 de intersección sobre r2. Desde r2 repetimos el proceso y obtenemos T2 sobre Γ y P3 sobre r3. Repetiremos el proceso hasta la obtención de Tn y Pn, que en este ejemplo son T4 y P4. Si hubiéramos acertado en la elección de P1, habiendo alcanzado la solución, sería Tn=4=T0. Lo cierto es que en general Tn=4 y T0 no coincidirán. Hemos obtenido un polígono con n-1 lados tangentes a la cónica exceptuando el lado n-ésimo y dos tangentes, desde el primer vértice P1 y el último Pn, que determinan sobre la cónica dos puntos T0 y Tn que si coinciden nos dan la solución del problema. Nosotros para establecer la solución estudiaremos la biyección hΓ:Γ→Γ entre T0 y Tn definida por hΓ(T0)=Tn y buscaremos la condición a cumplir para que dichos puntos coincidan. Si hΓ:Γ→Γ fuera una homografía de la cónica sobre sí misma, los puntos dobles (hΓ(T0)=T0) nos darían la solución. Diremos que la homografía existe y lo demostraremos en el teorema 4.1. |
||||
|
||||
1. PASOS A SEGUIR |
||||
|
||||
Polo y polar El hecho de trazar tangentes desde puntos de una recta a la cónica tiene mucho que ver con los conceptos de POLO y POLAR que se introducen estudiando algunas propiedades de cuerdas de la cónica (si observamos la INTRODUCCION vemos que T0 y T4 determinan una cuerda de Γ).
El concepto de POLO lo veremos en el teorema 2.5 y el de POLAR en el teorema 2.6. Para establecerlos veremos primero cuatro teoremas auxiliares: |
||||
teorema 2.1 |
Recíproco de la definición de proyección entre haces de rectas. Util para determinar alineaciones. |
|||
teorema 2.2 |
A partir del SEGUNDO TEOREMA DE DESARGUES establecemos las propiedades armónicas de las diagonales del cuadrilátero. |
|||
teorema 2.3 |
Dual del SEGUNDO TEOREMA DE DESARGUES EXTENDIDO A LAS CONICAS. Involuciones a partir del cuadrilátero circunscrito y la cónica. |
|||
teorema 2.4 |
Corolario del TEOREMA DE BRIANCHON. Relación entre diagonales y cuerdas que unen los puntos de contacto de un cuadrilátero circunscrito a una cónica. |
|||
Habiendo definido los conceptos de POLO y POLAR, introduciremos diferentes maneras de determinarlos y así completaremos el punto 2.
Involución de una cónica sobre sí misma El objetivo del punto 3 es determinar una caracterización de las involuciones, se establece en el COROLARIO 3.6 y nos ayudará a establecer la homografía buscada.
Para ello estableceremos una relación entre las involuciones del plano y las homologías armónicas del plano. teorema 3.1 y teorema 3.2.
En los teoremas 3.3 y 3.4, definiremos la homografía de una cónica sobre sí misma y estableceremos la existencia del eje y del centro de homografía que nos serán útiles para determinar la imagen de un punto por la homografía y los puntos fijos (o dobles).
Definiremos la INVOLUCIÓN de una cónica sobre sí misma que como involución del plano vincularemos con la HOMOLOGÍA ARMÓNICA.
En el teorema 3.5, identificaremos al eje y al centro de la involución como el eje y el centro de la homología armónica y deduciremos así la caracterización que buscamos en los,
COROLARIO 3.6 Y COROLARIO 3.7
La aplicación del teorema 2.6 tercero y el COROLARIO 3.6 para demostrar el teorema 4.1 nos permitirá hallar, en el punto 4, la homografía que resuelve el problema y desarrollar el MÉTODO DE SOLUCIÓN en el punto 5.
En los teoremas 6.3 y 6.4, del punto 6, consideraremos el caso en el que pueda haber más de dos soluciones. Si eso ocurre, existen infinitas soluciones y estableceremos cual es la configuración de las rectas dadas para que eso ocurra . Esta configuración tiene que ver con el concepto de triángulo autopolar (autoconjugado, autorrecíproco o conjugado) respecto a una cónica. De su definición y métodos de construcción deduciremos los teoremas 6.1 y 6.2,
La correlación con el problema original de Castillón se destaca en las CONCLUSIONES ( punto 7) |
||||
|
||||
2. POLOS Y POLARES |
||||
|
||||
Teorema 2.1 Cuando dos haces de cuatro rectas que se corresponden una a una, respectivamente, tienen sus razones dobles iguales (son homográficas), si una de las rectas coincide con su imagen, las tres rectas restantes del haz cortan a sus rectas correspondientes en el otro haz en tres puntos situados en línea recta.
(El teorema recíproco no es más que la definición de una proyección entre haces de rectas.) |
||||
|
||||
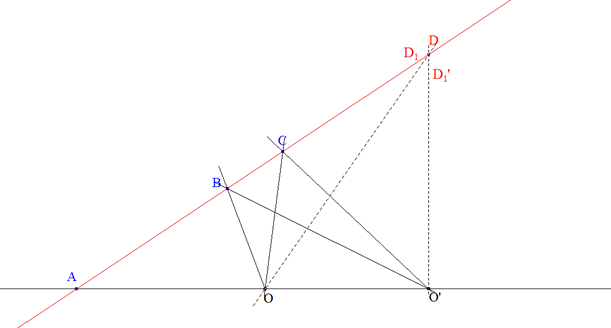 figura 2 figura 2
|
||||
Demostración 2.1 Sean O* y O’* los dos haces. Sean OA, OB, OC, OD (figura 2)las cuatro rectas de O* y O’A, O’B, O’C, O’D las cuatro rectas de O’* que les corresponden respectivamente. Supongamos que las rectas que coinciden son OA y O’A; entonces mostraremos que los puntos de intersección de cada recta con su correspondiente, B=OB∩O’B, C=OC∩O’C, D=OD∩O’D, están en línea recta.
Sean A=BC∩OO’, D1=BC∩OD y D1'=BC∩O'D. Como los dos haces son homográficos, conservan la razón doble; tenemos (OA, OB, OC, OD1)=(O’A, O’B, O’C, O' D1')y por lo tanto D1=D1' con lo que OD y O’D se cortan en BC. |
||||
|
||||
Si recordamos ahora el SEGUNDO TEOREMA DE DESARGUES, resolución del problema 183, sea un cuadrángulo ABCD y sea r una recta que no pasa por ninguno de sus vértices. Los lados opuestos del cuadrángulo cortan a r en puntos que se corresponden en una misma involución; podemos establecer el siguiente |
||||
|
||||
Teorema 2.2 En todo cuadrilátero, las dos diagonales dividen armónicamente la recta que une los puntos de encuentro de los lados opuestos. |
||||
|
||||
Demostración 2.2 Es una simple consecuencia del segundo teorema de Desargues; basta con tomar como transversal r la
recta que une los puntos de encuentro de los lados opuestos; cada uno de esos puntos será un punto
doble de la involución; además en una involución σ de puntos doble A y B, la razón doble cumple, para
todo punto P, (A, B, P, σ(P)) = -1, (problema 183), que al fin y al cabo es la condición de que P y σ(P)sean conjugados
armónicos.
|
||||
|
||||
La EXTENSIÓN DEL SEGUNDO TEOREMA DE DESARGUES A LAS CÓNICAS nos dice que: Cuando un cuadrilátero está inscrito a una cónica, una transversal cualquiera r encuentra a los dos pares de lados opuestos y a la cónica en tres pares de puntos homólogos en una involución de la recta r. Pero en este caso, nos interesa más el dual. |
||||
|
||||
Teorema 2.3 (correlativo del segundo teorema de Desargues extendido a las cónicas) Cuando tenemos un cuadrilátero circunscrito a una cónica, si desde un punto O trazamos rectas por los vértices y las dos tangentes a la curva, entonces esas tangentes y los pares de rectas por vértices opuestos del cuadrilátero, son rectas homólogas en una involución del haz O* de rectas concurrentes en O. |
||||
|
||||
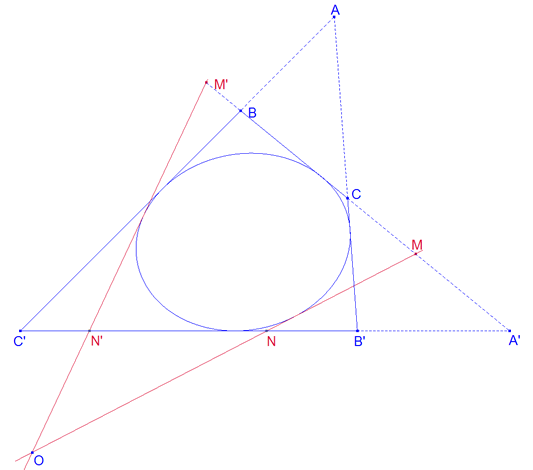 figura 3 figura 3
|
||||
Demostración 2.3 Consideremos ahora el caudrilátero completo, definido por sus vértices opuestos (A,A’), (B,B’), (C,C’), cuyos cuatro lados son tangentes a una cónica (figura 3). Por O, trazamos las tangentes a la cónica, las cuales encuentran a lado A’BC en M, M’ y al lado A’B’C’ en los puntos N, N’. Los puntos de encuentro entre las tangentes AB’, AC’, OM, OM’ y las dos tangentes A’B y A’B’ definirán una homografía (basta recordar, (problema 182) ,el enunciado alternativo del teorema fundamental de las tangentes a una cónica: Los puntos de intersección de una tangente móvil con dos tangentes fijas son homográficos). Las rectas desde O a estos puntos formarán dos haces homográficos.
La homografía conserva la razón doble, (C, B, M, M’)= (B’, C’, N, N’) y en el haz O* (OC, OB, OM, OM’)=(OB’,OC’,ON, ON’)=(OB’, OC’, OM, OM’) permutando (OB’, OC’, OM, OM’)=(OC’, OB’, OM’,OM) de lo que se deduce (OC, OB, OM, OM’)=(OC’, OB’, OM’,OM) entonces (OB, OB’), (OC, OC’), (OM, OM’) están en involución como vimos en el problema 183 al demostrar el segundo teorema de Desargues.
Vemos que OM y OM’ también son rectas homólogas en la involución definida por los pares (OB, OB’) y (OC, OC’); propiedad que también atañe a (OA, OA’).
Concluímos que los pares de rectas (OA, OA’),(OB, OB’),(OC, OC’),(OM, OM’) son pares de rectas homólogas de dos haces en involución. |
||||
|
||||
Si recordamos ahora el TEOREMA DE BRIANCHON Cuando un hexágono está circunscrito a una cónica, las diagonales que unen los vértices opuestos pasan por un mismo punto; y si en un cuadrilátero circunscrito a una cónica, consideramos los puntos de contacto de dos lados opuestos como dos vértices de un hexágono circunscrito, se deduce el |
||||
|
||||
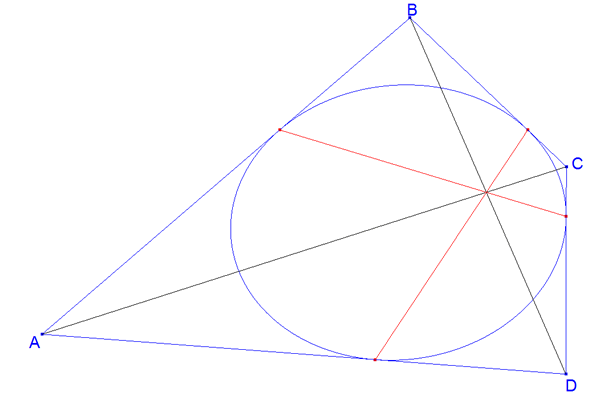 figura 4 figura 4 |
||||
Teorema 2.4 (corolario del teorema de Brianchon) En un cuadrilátero circunscrito a una cónica (figura 4), las rectas que unen los puntos de contacto de los lados opuestos pasan por el punto de encuentro de las dos diagonales. |
||||
|
||||
Después de estos cuatro primeros teoremas ya tenemos lo necesario para atacar la definición de POLAR de un punto. |
||||
|
||||
Teorema 2.5 (polar de un punto) Cuando varias cuerdas de una cónica pasan por un mismo punto: |
||||
primero |
Los puntos de encuentro de las rectas que unen dos a dos los extremos de dos cuerdas cualesquiera están sobre una misma recta. |
|||
segundo |
Las tangentes a los extremos de cada cuerda se cortan sobre esta recta. |
|||
tercero |
Esta recta es el lugar de los puntos conjugados armónicos del punto de encuentro de las cuerdas con respecto a los extremos de cada cuerda. |
|||
|
||||
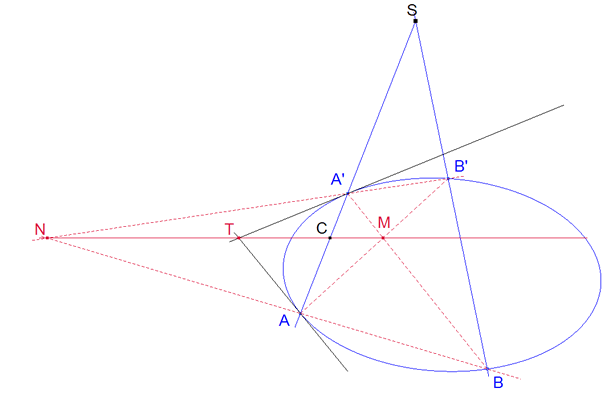 figura 5 figura 5
|
||||
Demostración 2.5 Sean AA’, BB’ dos cuerdas y S su punto de encuentro (figura 5). Probemos primero que los puntos M, N intersección de las rectas que unen los extremos de estas dos cuerdas y el punto T de encuentro de las tangentes por los extremos A, A’, de una de las cuerdas, son tres puntos en línea recta.
Como son puntos y tangentes de la misma cónica, el haz de rectas AT, AB, AB’, AA’ es homográfico al haz A’A, A’B, A’B’, A’T lo cual supone la igualdad de razones dobles
(AT,AB,AB’,AA’)=(A’A,A’B,A’B’,A’T)=(A’T,A’B’,A’B,A’A),
de donde AA’ coincide con su imagen A’A y por tanto, según el teorema 2.1 los puntos T=AT∩A’T, N=AB∩A’B’, M=AB’∩A’B están en línea recta.
Teniendo ahora en cuenta el teorema 2.2, para el cuadrilátero AMA’N, la intersección de las diagonales C=AA’∩MN es el conjugado armónico con respecto a los vértices A y A’ del punto S en el que la recta, que une los puntos de encuentro de los lados opuestos del cuadrilátero B,B’, encuentra a la diagonal AA’.
La recta MN se determina por medio de una sola cuerda AA’, ya que pasa por T punto de encuentro de las tangentes por A y A’ y por C, conjugado armónico de S respecto a A y A’.
La recta MN es la POLAR del punto S y el punto, a su vez, POLO de la recta.
Las rectas desde el polo a un punto de encuentro de la polar con la cónica es la tangente a la cónica en ese punto; si no fuera tangente, tendría otro punto diferente de encuentro con la cónica y el conjugado armónico de S respecto a estos dos puntos no sería el supuesto. |
||||
|
||||
Determinación de la polar de un punto S. Visto lo precedente podemos establecer 5 maneras distintas de hacerlo: |
||||
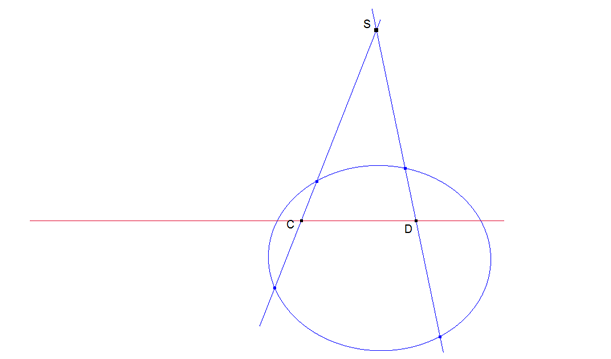 figura 6 figura 6
|
||||
primera manera (figura 6) Trazando por S dos transversales a la cónica y trazando, en cada una, el conjugado armónico de S con respecto a los dos puntos en que cada una de la rectas encuentra la cónica: la recta que une los dos puntos así determinados es la polar. |
||||
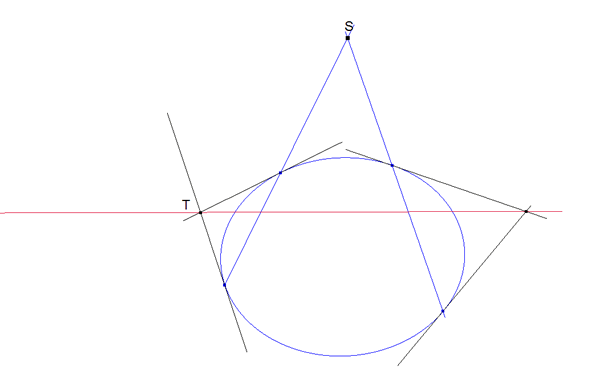 figura 7 figura 7
|
||||
segunda manera (figura 7) Trazando las tangentes por los puntos de intersección de cada transversal con la cónica; los puntos de encuentro de cada par de tangentes están sobre la polar. |
||||
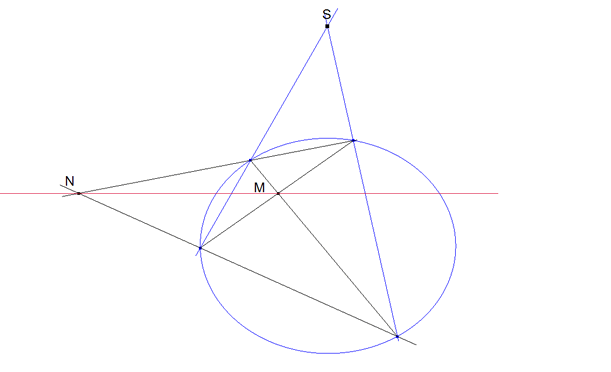 figura 8 figura 8
|
||||
tercera manera (figura 8) Uniendo dos a dos los puntos los puntos de encuentro de las transversales y la cónica por medio de rectas; los puntos de encuentro de estas rectas están en la polar. |
||||
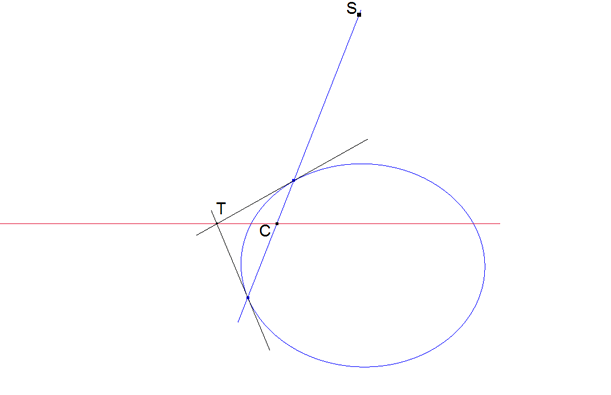 figura 9 figura 9
|
||||
cuarta manera (figura 9) Con una sola transversal; el conjugado armónico de S con respecto a los puntos de encuentro de la transversal con la cónica y el de intersección de las tangentes en dichos puntos determinan la polar. |
||||
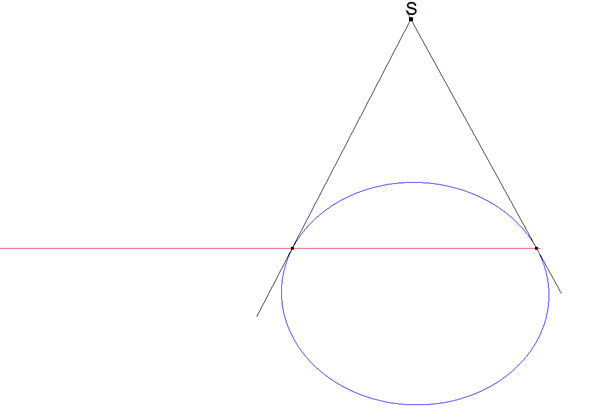 figura 10 figura 10
|
||||
quinta manera (figura 10) Trazando por S dos tangentes a la cónica; la recta que une los dos puntos de contacto es la polar. |
||||
|
||||
Teorema 2.6 (polo de una recta) Si, por cada punto de una recta s, se trazan dos tangentes a una cónica y sea c la conjugada armónica de s con respecto a las dos tangentes: |
||||
primero |
Todas las rectas c pasan por un mismo punto S. |
|||
segundo |
Las diagonales del cuadrilátero formado por las cuatro tangentes desde dos puntos de la recta s pasan por S. |
|||
tercero |
Las cuerdas que unen los puntos de contacto de las tangentes trazadas desde cada punto de la recta s pasan también por S. |
|||
cuarto |
El punto S es el polo de la recta s. |
|||
|
||||
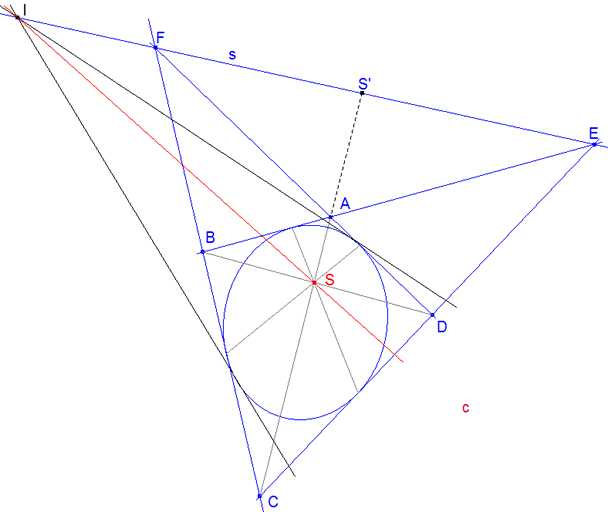 figura 11 figura 11
|
||||
Demostración 2.6 (figura 11) Sea ABCD el cuadrilátero formado por las tangentes a la cónica desde dos puntos E y F de la recta s. Demostraremos que si por I, otro punto de s, trazamos la recta conjugada armónica c de s respecto a las dos tangentes trazadas por I, c pasará por S el punto de encuentro de las diagonales de ABCD.
Las dos tangentes desde I y las dos rectas desde este punto a los vértices opuestos (A,C) del cuadrilátero definen una involución teorema 2.3, en la que la recta IE=s es doble. Esta y la otra recta doble son conjugadas armónicas con respecto a las dos rectas IA, IC. Ya que en el cuadrilátero ABCD, los vértices opuestos A, C son conjugados armónicos respecto a los al punto S y al punto S’ donde la diagonal AC encuentra a la recta EF=s (teorema 2.2). Esta recta IS y la primera IE son conjugadas armónicas respecto a las dos tangentes a la cónica. Esto demuestra el primer apartado.
Como el punto, por el cual pasan todas las rectas c, es punto de encuentro de las diagonales del cuadrilátero formado por las tangentes por dos puntos arbitrarios de s; hemos probado el segundo apartado.
El tercer apartado es consecuencia del segundo; ya que si E, F llegan a confundirse, una de las diagonales del cuadrilátero se convierte en la cuerda de contacto de sus dos lados por el punto E. Además ya se ha visto que (teorema 2.4), en el cuadrilátero circunscrito, las rectas que unen los puntos de contacto de los lados opuestos pasan por el punto de encuentro de dos diagonales.
Que s es la polar de S se obtiene del hecho de que las tangentes a la cónica por los extremos de las cuerdas por S se cruzan en E, F, ... sobre la recta.
Cuando la recta s corta a la cónica en dos puntos, el polo de la recta es el punto de encuentro de las tangentes por esos puntos. |
||||
|
||||
Determinación del polo de una recta s. Visto lo precedente podemos establecer 5 maneras distintas de hacerlo: |
||||
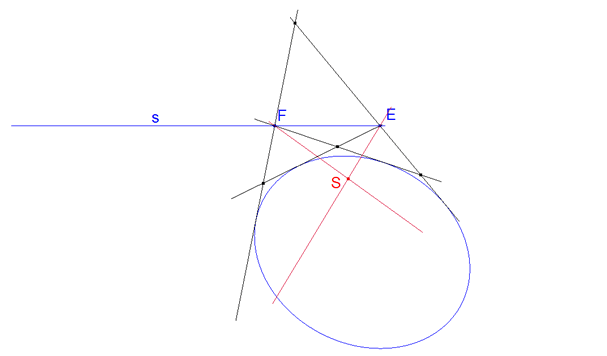 figura 12 figura 12
|
||||
primera manera (figura 12) Si Trazamos por dos puntos de s las tangentes a la cónica, las conjugadas armónicas de s, con respecto a cada par de tangentes, se encuentran en el polo buscado. |
||||
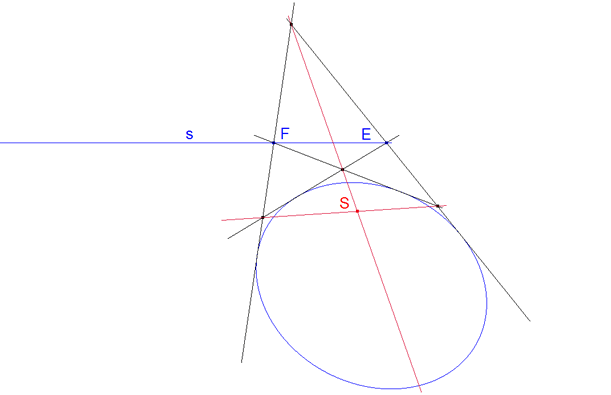 figura 13 figura 13
|
||||
segunda manera (figura 13) El punto de encuentro de las dos diagonales del cuadrilátero formado por las cuatro tangentes es el polo buscado. |
||||
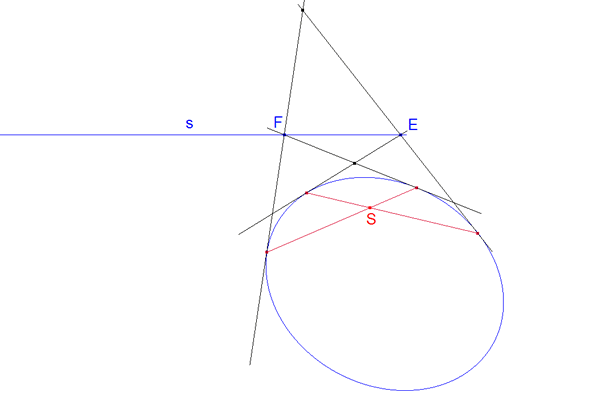 figura 14 figura 14
|
||||
tercera manera (figura 14) El punto de encuentro de las dos cuerdas de contacto de los dos pares de tangentes es el polo buscado. |
||||
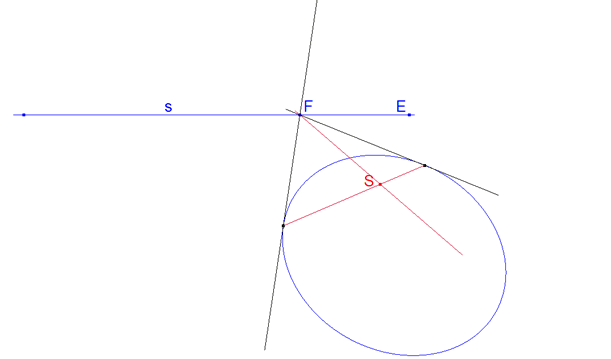 figura 15 figura 15
|
||||
cuarta manera (figura 15) Se trazan desde un solo punto de la recta las dos tangentes a la curva y la conjugada armónica de s respecto estas tangentes. El punto de encuentro entre esta conjugada armónica y la cuerda que une los puntos de contacto es el polo S. |
||||
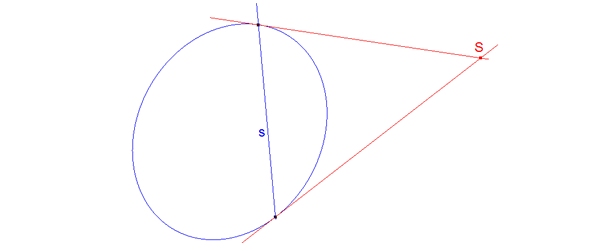 figura 16 figura 16
|
||||
quinta manera (figura 16) Por último, si por los puntos de encuentro de la recta con la cónica trazamos las tangentes, éstas se encuentran en el polo. |
||||
|
||||
3. INVOLUCION DE UNA CONICA SOBRE SI MISMA |
||||
|
||||
Homografía en el plano Aunque podríamos aprovechar que la recta proyectiva y la cónica son isomorfas, apéndice al problema 137, y por lo tanto aplicar lo conocido para la recta proyectiva a la cónica; el estudio se hará directamente en el plano. Veremos que la involución de una cónica sobre sí misma es una homología (armónica) y ello nos llevará a la caracterización de las involuciones de una cónica sobre sí misma que nos permitirá resolver el problema original.
Recordamos que una homografía del plano es una biyección del plano sobre sí mismo que conserva la razón doble.
Homología en el plano, (resolución del problema 167) Recordemos que una homografía plana, en la que existe una recta s de puntos fijos y S* un haz de rectas fijas concurrentes en un punto S, recibe el nombre de homología de eje s y centro S. |
||||
|
||||
Teorema 3.1 Sea ahora AA’ y BB’ dos pares de puntos homólogos en una homología de centro S y eje s. Si A"= AA’∩ s y B"= BB’∩ s entonces se cumple la igualdad de razones dobles
(A, A’, S, A")=(B ,B’, S, B")
Esta razón doble constante se denomina invariante homológico. |
||||
|
||||
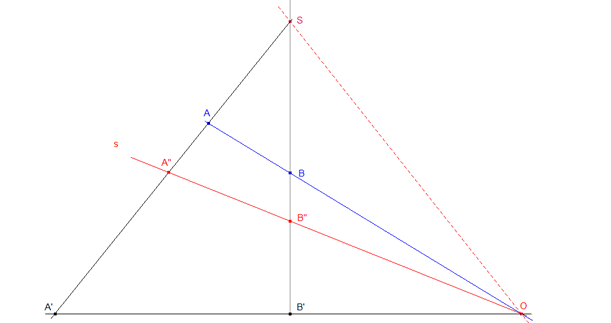 figura 17 figura 17
|
||||
Demostración 3.1 Tomando el haz de rectas O*, O=AB∩A’ B’, vemos (figura 17) que por ser una homología, entonces el punto O está sobre la recta s y (OA’,OA",OA,OS)=(OB’,OB",OB,OS) lo que significa que (OA,OA’,OS,OA")=(OB,OB’,OS,OB") y de aquí (A, A’, S, A")=(B, B’, S, B").
Si (A, A’, S, A")= -1, la homología se llama armónica. |
||||
|
||||
Involución en el plano Una homografía plana h, que se supone no idéntica, tal que h=h-1 es una involución. |
||||
|
||||
Teorema 3.2 Toda involución del plano es una homología armónica y recíprocamente |
||||
|
||||
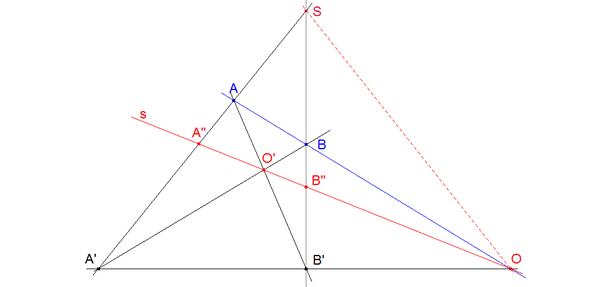 figura 18 figura 18
|
||||
Demostración 3.2 (directo) Si observamos la homología h del apartado anterior suponiéndola armónica y considerando los puntos A, A’, S, A", vemos que h(A)=A’, S es un punto fijo y A" es otro punto fijo pues se halla sobre el eje se homología que es una recta de puntos fijos y como la homología deja invariante la recta SA", y tiene dos puntos fijos en ella, y como
(S, A",A, A’)=-1 (por ser armónica);
y además según hemos visto en el problema 183, esta razón doble define una involución σ de puntos dobles S y A" y σ(A)=A’ y por tanto h=σ.
(recíproco) Sea ahora una involución σ distinta de la identidad, entonces es seguro que existe una recta r que no coincide con σ(r). Podemos pues encontrar dos puntos A, B cualesquiera del plano con σ(A)=A’ y σ(B)=B’ que no están sobre la recta AB. Sea S=AA’∩BB’, O=AB∩A’B’ y O’=AB’∩A’B (figura 18). Sea h la homología de centro S y eje OO’=s que transforma A en A’. Entonces σ y h coinciden en cuatro puntos A, A’, B, B’ y por lo tanto σ=h. |
||||
|
||||
Homografía de una cónica sobre sí misma Denominamos homografía de una cónica sobre sí misma a una biyección de Γ→Γ que deja invariante la razón doble de cuatro puntos cualesquiera de Γ.
Es fácil demostrar, ver Sidler Géométrie projective..., que toda homografía plana que deja invariante una cónica Γ define por restricción una homografía de Γ. Recíprocamente, toda homografía de Γ se prolonga de manera única en una homografía plana que deja Γ invariante. |
||||
|
||||
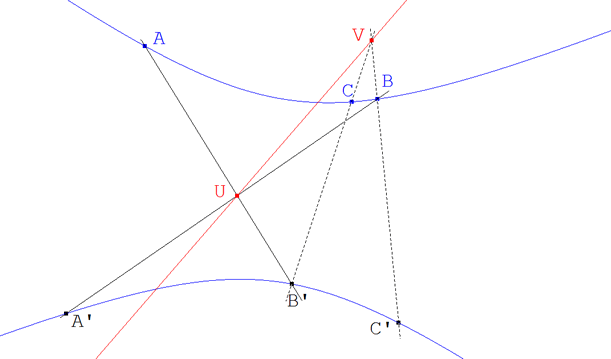 figura 19 figura 19
|
||||
Teorema 3.3 (Eje de homografía de una cónica sobre sí misma) Sea hΓ una homografía de una cónica sobre sí misma. A, B dos puntos distintos de la cónica y A’ y B’ sus imágenes. AB’ ∩ BA’ está en una recta fija que recibe el nombre de eje de homografía.
Los puntos fijos de la homografía son los de intersección del eje de homografía con la cónica. |
||||
|
||||
Demostración 3.3 Sea A un punto de Γ distinto de su imagen homográfica A’ y sea B un punto cualquiera de la cónica y B’ su imagen por la homografía. La correspondencia entre haces de rectas h*:A’*→A* con h*(A’B)=AB conserva la razón doble y por tanto es una homografía. En esta homografía h*(A’A)=AA’ y de acuerdo con el teorema 2.1 el lugar de los puntos de intersección AB’∩A’B es una recta. |
||||
|
||||
Teorema 3.4 (Centro de homografía. Dual del teorema 3.3) Sea hΓ* una homografía de la cónica sobre sí misma y a, b dos tangentes distintas de la cónica y a’ y b’ sus imágenes. La recta que une los puntos a∩b’ y b∩a’ pasa por un punto fijo que recibe el nombre de centro de homografía. |
||||
|
||||
Construcción de la imagen de un punto de la cónica por la homografía. Dado el eje de homografía u y un punto A de Γ con imagen A’, para todo punto B de Γ el teorema 3.3 nos proporciona un método par obtener B’=hΓ(B). Obtenemos U=BA’∩u entonces B’=BU∩Γ. (Ver figura 19).
Hallar los puntos dobles de la homografía de una cónica sobre sí misma. Si, en el párrafo anterior, U está sobre Γ, será A=U=A’=u∩Γ y por lo tanto los puntos dobles son los de intersección del eje de homografía u con la cónica Γ.
Relación con la polaridad Como (Demostración 2.5) la polar de un punto de Γ es la tangente en ese punto, vemos que el eje de homografía es la polar del centro de homografía y el centro de homografía el polo del eje de homografía. (Si observamos la quinta manera de determinar el polo de una recta, vemos que las tangentes en los puntos de intersección de la polar se cortan en el polo; por tanto, las tangentes en en los puntos dobles se cortan en el centro de homografía.)
Estamos ahora en disposición de ver la involución de una cónica sobre sí misma. |
||||
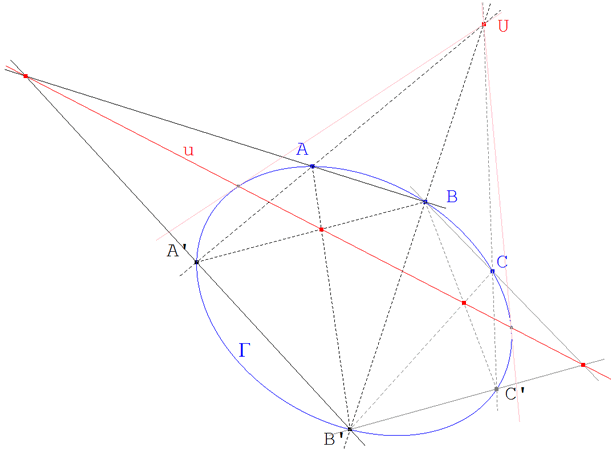 figura 20 figura 20
|
||||
Involución de una cónica sobre sí misma Se dice que una homografía σΓ:Γ→Γ de una cónica sobre sí misma es una INVOLUCION si es distinta de la identidad y si (σΓ◦σΓ) es la aplicación idéntica de Γ (es decir σΓ-1=σΓ).
Si σΓ es una involución, entonces P'=σΓ(P) y P=σΓ(P'). Se dice que la involución intercambia los puntos P y P' o que P y P' son homólogos en la involución σΓ.
Esta involución σΓ de la cónica, como homografía, está subordinada (como hemos dicho) a una homografía σ del plano que deja invariante a la cónica Γ. Considerando la homografía plana σ, las rectas que unen puntos homólogos de la cónica (figura 20) serán rectas fijas (se transforman en sí mismas). Al mismo tiempo, las rectas homólogas se encuentran también en puntos fijos. Pero la homografía que posee una infinidad de rectas fijas y de puntos fijos es una homología.
Por lo tanto, las rectas que unen los puntos homólogos de la involución pasarán por el centro de homología U y las rectas homólogss se encuentran en el eje de la homología u (figura 20); pero eso es una de las manera de determinar que u es la polar de U (teorema 2.5). Deducimos que el eje de homología u es la polar, respecto a la cónica Γ, del centro de homología U. Esta es pues la homología armónica (teorema 2.5 tercero y demostración 3.1) que se identifica con la involución (teorema 3.2)
De lo anterior, podemos concluir el siguiente |
||||
|
||||
Teorema 3.5 Una involución σΓ:Γ→Γ, de una cónica sobre sí misma, está subordinada a una homología armónica σ que deja invariante la cónica Γ y tiene por centro y eje de homología (U, u) al centro y eje de homografía de la involución. |
||||
|
||||
Demostración 3.5 (figura 20) La identificación de involución y homología está establecida en el teorema 3.2.
Si σΓ(A)=A’ y σΓ(B)=B’ son pares de puntos homólogos en la involución (situados en las rectas que pasan por U), las rectas AB’ y BA’ las rectas AB y A’B’ se encuentran sobre el eje de homografía quedando así determinado dicho eje. Pero esos mismos puntos se encuentran sobre el eje de homología u y lo determinan. Deducimos que el eje de homografía de la involución coincide con el eje de la homología armónica correspondiente.
Correlativamente, U (polo de u) es además el centro de homografía. |
||||
|
||||
Y de aquí deducimos directamente los siguientes corolarios (duales entre sí): |
||||
|
||||
COROLARIO 3.6 Los pares de puntos, de una cónica Γ, SITUADOS SOBRE RECTAS QUE PASAN POR UN PUNTO FIJO (será el centro de homografía de la involución) DETERMINAN UNA INVOLUCIÓN σΓ:Γ→Γ DE LA CÓNICA SOBRE SÍ MISMA. |
||||
|
||||
COROLARIO 3.7 (dual del 3.6) Los pares de tangentes, auna cónica Γ, QUE SE CORTAN SOBRE LOS PUNTOS DE UNA RECTA FIJA (será el centro de homografía de la involución) CONSTITUYEN UNA INVOLUCION σΓ:Γ*→Γ* DE LA CONICA SOBRE SI MISMA.
(Γ* es la cónica envolvente de tangentes, dual de Γ lugar de puntos) |
||||
|
||||
4. DETERMINACION DE LA HOMOGRAFIA |
||||
|
||||
Teorema 4.1 Cuando un polígono de n lados, cuyos n vértices deslizan sobre n rectas fijas cualesquiera, tiene todos sus lados, excepto uno, tangentes a una cónica, si por los dos vértices situados sobre este último lado se llevan dos tangentes a la cónica, los puntos de contacto definen una homografía de la cónica sobre sí misma. |
||||
|
||||
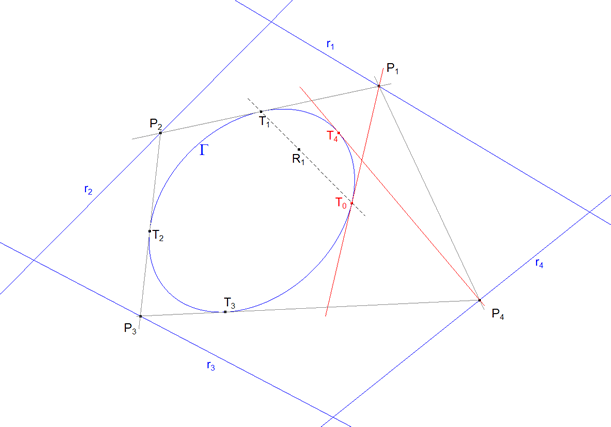 figura 21 figura 21
|
||||
Demostración 4.1 Retomando la figura 1 de la INTRODUCCION, consideremos el cuadrilátero (n=4) de vértices P1, P2, P3, P4=n en el que los tres (n-1) lados P1P2, P2P3, P3P4 deslizan tangentes a una cónica. Demostremos que existe una homografía hΓ:Γ→Γ de la cónica sobre sí misma tal que hΓ(T0)=T4=n, siendo T0 y T4=n los puntos de contacto a los que se refiere el teorema (figura 21). |
||||
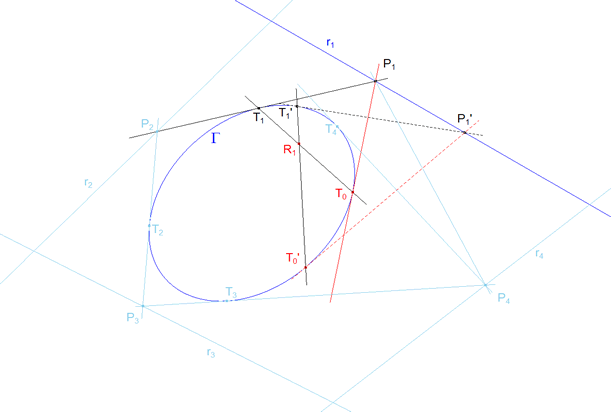 figura 22 figura 22
|
||||
Si consideramos los n-1 primeros puntos de contacto T1, T2 y T3=n-1 de los lados P1P2, P2P3, P3P4=n con la cónica Γ, podemos concluir que si desplazamos P1 sobre r1 la cuerda T1T0 gira en torno a R1 (figura 22) que es el polo de la recta r1 respecto a la cónica (teorema 2.6 tercero) y aplicando el COROLARIO 3.6, como R1 es fijo, T1 y T0 definen una involución σ1Γ:Γ→Γ de la cónica sobre sí misma con σ1Γ(T0)=T1.
Del mismo modo definiremos
Si Ri es el polo de la recta ri respecto la cónica Γ, la definición de σiΓ es
Y como la composición de homografías es una homografía podemos obtener
y por tanto la homografía buscada no es más que la composición de las n involuciones definidas en este párrafo
|
||||
|
||||
5. SOLUCION PARA EL TRIANGULO (n=3) |
||||
|
||||
5.1 Determinación de la homografía 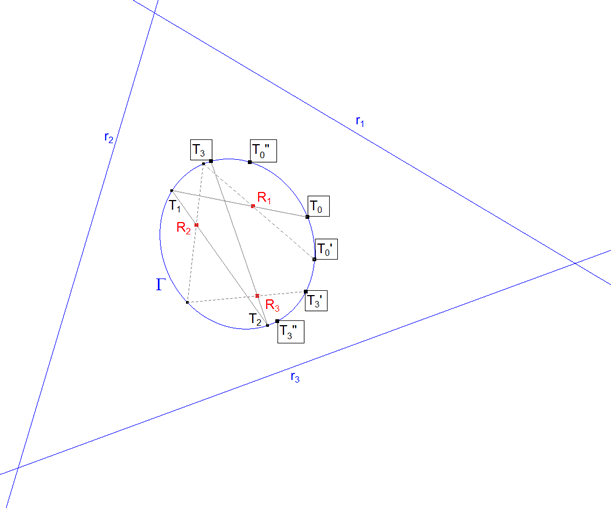 figura 23 figura 23Determinamos una homografía hΓ:Γ→Γ de una cónica Γ sobre sí misma por medio de tres puntos de Γ distintos T0, T’0, T”0 y sus imágenes T3, T’3, T”3.
Procederíamos como en la INTRODUCCION, trazaríamos las tangentes y obtendríamos los puntos de contacto.
Pero hay un camino mucho más fácil; esta homografía, como hemos visto, es composición de involuciones con centro de involución en el polo de la recta correspondiente.
Hallados entonces los polos R1, R2 y R3 respecto a la cónica Γ de r1, r2 y r3, para obtener la imagen por la homografía de un punto de la cónica: |
||||
a |
basta tomar un punto T0 sobre Γ |
|||
b |
y hallar σ1Γ(T0)=T1=T0R1∩Γ, |
|||
c |
luego T2=T1R2∩Γ |
|||
d |
y T3=T2R3∩Γ. Igualmente hallamos T’3 imagen de T’0 y T”3 imagen de T”0. |
|||
|
||||
5.2 Determinación de los puntos fijos. Eje de homografía 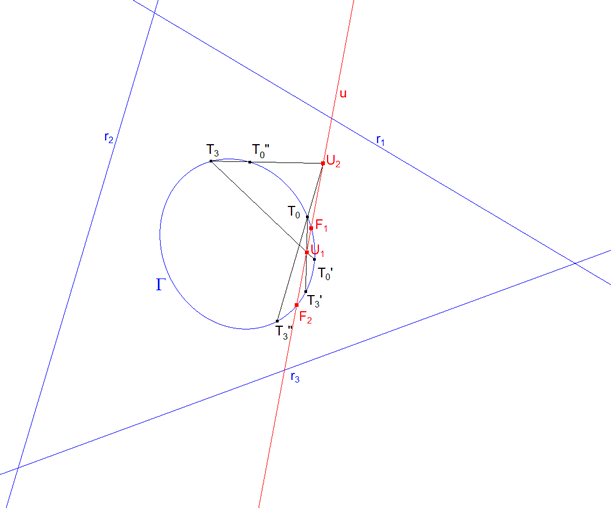 figura 24 figura 24Dada la homografía hΓ:Γ→Γ de una cónica Γ sobre sí misma, los puntos T0 de Γ, tales que hΓ(T0)=T0, se denominan puntos fijos o dobles y como hemos visto son los de intersección entre el eje de homografía u y la cónica Γ.
Habrá pues cero, uno o dos puntos fijos, según el eje no corte, sea tangente o corte a la cónica. (Existe casos con infinitas soluciones)
Para seguir con la solución hallaremos el eje de homografía u siguiendo los pasos detallados en el teorema 3.3 |
||||
e |
hallamos U1=T0T3'∩T3T0' |
|||
f |
hallamos U2=T0T3"∩T3T0" |
|||
g |
luego u=U1U2 |
|||
h |
(F1, F2 )=u∩Γ son los puntos fijos buscados. |
|||
|
||||
5.3 Determinación de los triángulos solución 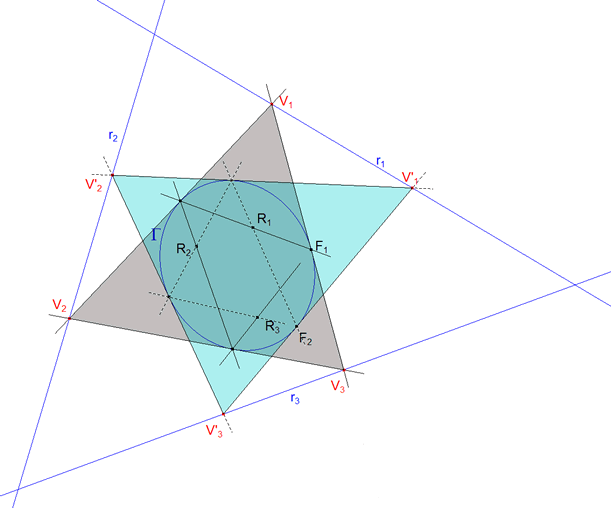 figura 25 figura 25Para hallar el primer triángulo partimos del primer punto fijo F1. |
||||
i |
trazamos la tangente t1 por F1 |
|||
j |
hallamos V1=t1∩r1 y V3=t1∩r3 |
|||
k |
ahora trazaríamos la tangente a la cónica Γ desde V1; pero es más fácil hallar F1R1∩Γ |
|||
l |
en lugar de la tangente mencionada trazamos desde V1 la recta por F1R1∩Γ |
|||
m |
hallamos V2 en su intersección con r2 |
|||
n |
uniendo V1, V2 y V3 obtenemos el primer triángulo |
|||
0 |
análogamente a partir de F2 obtendríamos V’1, V’2 y V’3 |
|||
|
||||
6. UNA CONFIGURACION QUE COMPORTA INFINITAS SOLUCIONES |
||||
|
||||
Supongamos que además de los puntos fijos F1 y F2existe un punto T ∈ Γ que también sea solución; entonces σ3Γºσ2Γºσ1Γ(T) =T.
Recordando que la recta proyectiva y la cónica son isomorfas, podemos decir que si dos homografías coinciden en tres puntos distintos son idénticas y como en este caso σ3Γºσ2Γºσ1Γ coincide con la identidad ιΓ en F1, F2 y T entonces σ3Γºσ2Γºσ1Γ = ιΓ ¡Para todo punto T ∈ Γ! y por tanto el problema tendría ¡infinitas soluciones!
Después de los conceptos de polo y polar, podemos preguntarnos: ¿Qué es un triángulo autopolar? Se dice que un triángulo es autopolar (autoconjugado o conjugado) respecto a una cónica si la polar de cada uno de sus vértices coincide con el lado opuesto, y del mismo modo el polo de cada uno de sus lados coincide con el vértice opuesto. |
||||
¿Cómo construir un triángulo autopolar (autoconjugado) respecto a una cónica dada Γ?
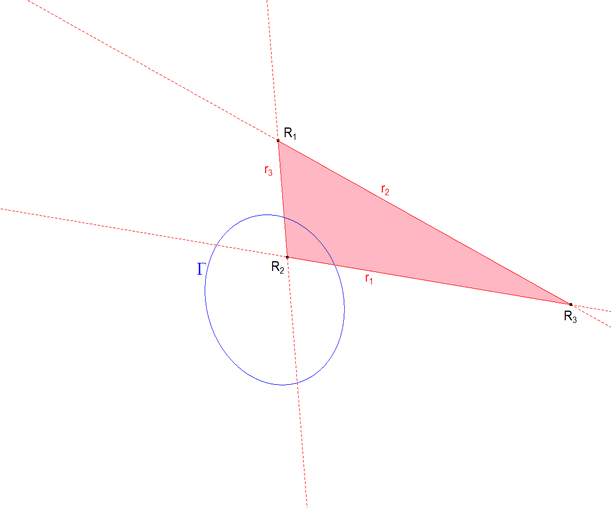 figura 26 figura 26 |
||||
primera manera (figura 26) Tomamos arbitraiamente un vértice R1 y trazamos su polar r1 y sobre ella un punto cualquiera R2 del que trazamos su polar r2. Ests última pasará por R1, ya que R1 y R2 son puntos conjugados; si R3 es el punto donde r2 corta a r1, entonces (R1,R3) y (R2,R3) son pares de puntos conjugados; entonces R1R2R3 es un triángulo autopolar.
segunda manera (figura 26) Tomada una recta cualquiera r1, trazamos su polo R1; si por R1, trazamos cualquier recta r2, su polo R2 estará sobre r1; y sea r3 la recta que une R1 y R2; entonces r1r2r3 es el triángulo requerido y las rectas r1, r2 , r3 son conjugadas dos a dos. |
||||
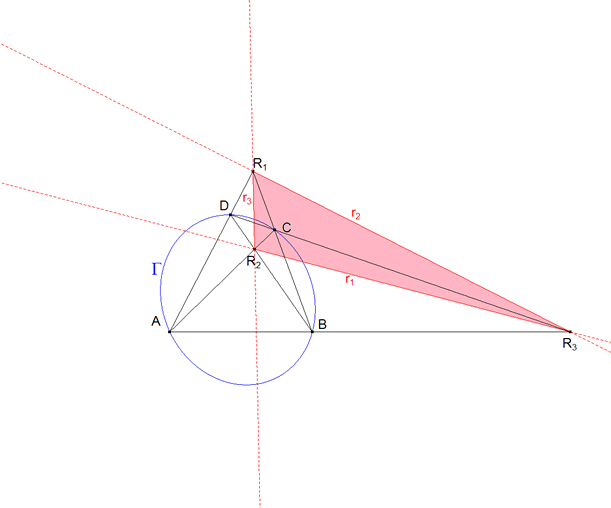 figura 27 figura 27 |
||||
tercera manera (figura 27) Desde un punto cualquiera R1 trazamos dos secantes que cortan a la cónica Γ en A, D y B, C respectivamente; AC y BD se cortan en R2 y AB y CD se cortan en R3; entonces R1R2R3 es un triángulo autopolar.
De esta construcción se deduce el siguiente
teorema 6.1 Los puntos de intersección de las diagonales de un cuadrivértice completo formado por cuatro puntos cualesquiera de una cónica son vértices de un triángulo autopolar respecto a la cónica. Y las diagonales del cuadrilátero formado por cuatro tangentes cualesquiera a la cónica son los lados de un triángulo autoconjugado con respecto a la cónica. |
||||
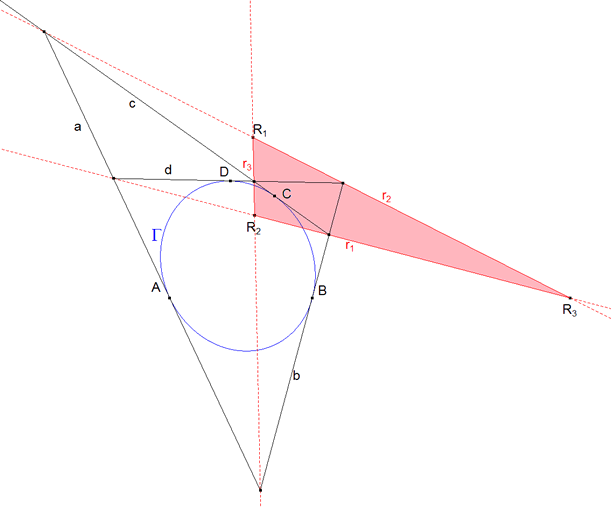 figura 28 figura 28 |
||||
cuarta manera (figura 28) De una recta cualquiera r1, tomamos dos puntos y desde ellos trazamos, a la cónica, dos pares de tangentes (a,d) y (b,c); sea r2 la recta que une a∩c y b∩d; sea r3 la recta que une a∩b y c∩d; entonces r1r2r3 es un triángulo autopolar.
De esta construcción se deduce el siguiente
teorema 6.2 El triángulo cuyos vértices son los puntos diagonales de un cuadrivértice completo es autoconjugado con respecto a la cónica circunscrita al cuadrivértice. Y el triángulo cuyos lados son las diagonales de un cuadrilátero completo es autoconjugado con respecto a la cónica inscrita en el cuadrilátero . |
||||
A partir de aquí ya podemos enunciar el
teorema 6.3 El producto de tres involuciones σRiΓºσRjΓºσRkΓ de centros distintos Ri, Rj, Rk es la identidad ιΓ si y sólo si el triángulo RiRjRk es autopolar.
 figura 29 figura 29
demostración 6.3 Veremos que si el producto de las tres involuciones es la identidad ιΓ entonces el producto de dos de ellas conmuta:
y como la identidad y cada involución es inversa de sí misma y por lo tanto Vemos además que el producto de dos de ellas, con centros respectivos en Ri y Rj, es una involución con centro en Rk. Recordando el corolario 3.6 y el teorema 6.1 para darnos cuenta que Rk es el polo de la recta que une Ri y Rj. Basta observar la figura 29 que no es más que una repetición de la figura 27.
Lo mismo se cumple permutando todos los índices y por lo tanto RiRjRk es autopolar.
Para el recíproco basta ver que del triángulo autopolar podríamos trazar el cuadrivértice o cuadrilátero correspondiente como se ve en la figura 29 y por lo tanto se cumpliría recordando, de nuevo, el corolario 3.6 y de aquí, por ejmplo
Un trabajo de FRANÇOIS RIDEAU sobre el problema de Castillón, publicado en dos partes en la revista Quadrature (la primera en el n°54 de y la segunda en el número de enero de 2005), expone de forma soberbia este apartado proporcionando enunciados y demostraciones rigurosas y elegantes. |
||||
7. CONCLUSIONES |
||||
|
||||
La solución, una vez deducida, es bastante sencilla; pero montar la justificación de la solución me ha costado lo suyo. La dificultad ( y la gracia) ha estado en que casi toda la bibliografía sobre Geometría Proyectiva siempre demuestra los teoremas que tratan de puntos y suelen dejar los duales para el lector.
El método que inicialmente me había propuesto era a base de trazar tangentes; pero la construcción, en Cabri, de las dos tangentes desde un punto a una cónica es inestable y por eso se me ocurrió usar los polos de las rectas, aprovechando las involuciones que componen la homografía que resuelve el problema.
De este modo, sorprendentemente, se ve clarísimo que es el dual del problema de Castillón y que los dos problemas son equivalentes. Resolver este problema, como se ha hecho, equivale a resolver el siguiente Problema de Castillón; inscribir un triángulo, a una cónica, cuyos lados pasen por tres puntos que sean los polos respecto a la cónica de las rectas dadas.
No he tenido la suerte de ver lo que hizo GERGONNE; pero si, por fortuna, alguien lo tuviera, pido por favor que se lo haga llegar a RICARDO BARROSO ¡Sabiendo que Gergonne no tenía Cabri, leerlo será edificante!
Tal vez falten unas notas donde detallar como se traza la tangente en un punto a una cónica, las dos tangentes desde un punto a una cónica y polos y polares. Excepto la tangente en un punto que se puede hacer muy fácil con el teorema de Pascal y viene junto con Cabri (en las figuras para macros), las demás se pueden deducir de los métodos que se dan en el problema. Evidentemente, todo lo expuesto aquí no es ciencia infusa. Como decía al principio, la idea de atacar este problema la saqué de Aperçu historique sur l’origine et le développement des méthodes en géométrie, Nota XI. de Michel Chasles.
La idea de buscar la homografía que resolviera el problema y la redacción de este teorema como polígonos cuyos vértices deslizan en rectas fijas... también es de Michel Chasles, Traité des Sections Coniques, Gauthier-Villars, París (1865). (Es la primera parte; pero es que no se llegó a publicar la segunda), quien quiera consultarlo y no lo tenga, lo puede ver en La Universidad de Michigan.
Pero para encontrar la homografía había que demostrar que en las involuciones, las rectas que unen un punto y su imagen pasan por un punto fijo. (Hay quien denomina a esto el teorema de Fregier; pero según parece, Fregier sólo atacó el caso de haces homográficos ortogonales). En todo caso, no me gustaba nada de lo que iba encontrando sobre el particular. Hasta que pensé, Jean-Claude Sidler Géométrie projective 2ª édition, Dunod, Paris 2000 , que mejor sería atacar las involuciones de una cónica sobre sí misma como homogrfías generales del plano.
El siguiente paso era como demostrar este tema del punto fijo de la recta entre un punto y su imagen por una involución. La mejor inspiración en un libro clásico, Leçons de Géométrie Projective, Federigo Enriques, réimpression de Jacques Gabay, Paris (1993). De nuevo, quien no lo tenga puede consultar La Universidad de Michigan . Con la ayuda de esta obra he establecido la identificación de la involución con la homología armónica.
Ese punto vinculado a las involuciones se puede identificar con el centro de giro de las cuerdas, entre los puntos de contacto, que se forman en la cónica durante la construcción de las dos tangentes a la misma desde un punto que recorre una recta; pero ese punto es el polo de la recta mencionada y con las propiedades de polar y polo, el problema quedaba muy simplificado. En este punto, pensé en introducir los conceptos de polo y polar; pero con la condición de hacerlo con la suficiente extensión para que me sirvieran de referencia de ahora en adelante. La introducción, a mi entender, más didáctica es la de Michel Chasles en su tratado de cónicas más arriba citado.
Para completar, faltaban el Segundo teorema de Desargues, el Teorema de Brianchon y otros teoremas auxiliares que pueden encontrarse en cualquier libro de Geometría Proyectiva e incluso en algunos de los problemas del Laboratorio virtual de triángulos con Cabri II de RICARDO BARROSO CAMPOS, como hemos indicado a lo largo de la página. Demostraciones muy sencillas de los mismos, en forma de ejercicios, también pueden encontrarse en Exercices de Géométrie Moderne, Georges Papelier, réimpression de Jacques Gabay, Paris (1996).
Las consideraciones para el caso de infinitas soluciones las aprendí, por primera vez de una comunicación personal de François Rideau sobre el problema de Castillón. Aunque las cuestiones del triángulo autopolar se exponen magníficamente en Elements of Projective Geometry, Luigi Cremona, Clarendon Press, Oxford (1885), esta obra puede consultarse en La Universidad de Michigan
En el método de solución desarrollado, empezamos la solución tomando un punto cualquiera de la cónica, lo que le resta algo de elegancia a la generalidad de la solución. En su artículo, François Rideau, basándose en la teoría de conjugación, desarrolla una resolución del problema directo de Castillón sin tener que partir de un punto arbitrario y usando sólo los datos del problema. Este artículo se ha publicado en el nº 54 de la revista Quadrature y su continuación en el número de enero de 2005. Pueden encontrarse su método desarrollado en CABRI en http://www.cabri.net/castillon/
Para acabar diría que se puede consultar casi todo en Traité de Géométrie Supérieure, Michel Chasles, Gauthier-Villars, Paris 1880, esta obra puede consultarse en La Universidad de Michigan y también en Gallica-Bibliothèque nationale de France. |