Áreas de Triángulos Tangenciales

Juan Carlos Salazar

Introducción

A partir de la aplicación de un conocido teorema que establece la relación entre las áreas de un triángulo y su triángulo tangencial interno en función de sus circunradios, cuya demostración no entregamos en este artículo, obtenemos algunas relaciones similares para otros casos que consideramos poco conocidos o quizás inéditos.

Teorema 1

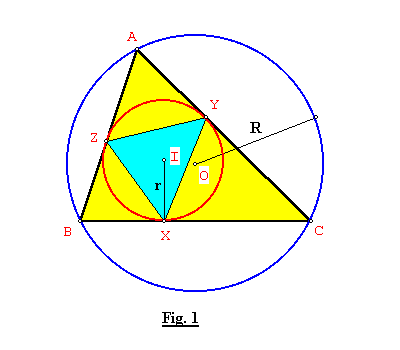
En un triángulo ABC de circunradio R, el círculo inscrito de radio r determina el triángulo XYZ, donde X, Y, Z son los puntos de tangencia del incírculo con los lados BC, CA, AB. Demostrar que: donde: [XYZ]= área de XYZ. (Ver Fig. 1).

Nota:

Una demostración de este interesante teorema se puede encontrar en la Revista Escolar de las Olimpiadas Iberoamericanas [1], que edita el Prof. Francisco Bellot Rosado.

Teorema 2:

Sea el triángulo acutángulo ABC, cuyo ortocentro es H. Los círculos inscritos (I, r), (I₁, r₁), (I₂, r₂), (I₃, r₃) correspondientes a los triángulos ABC, BHC, AHC y AHB determinan los triángulos tangenciales  internos de áreas S, S₁, S₂, S₃ correspondientes.

Demostrar que:

Demostración: Ver Fig. 2.

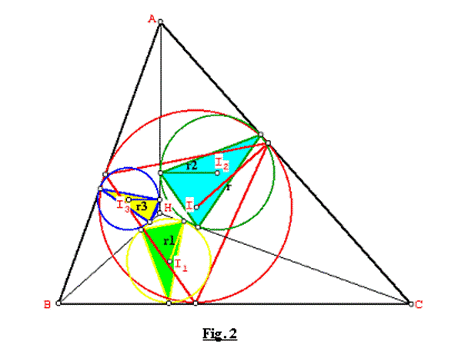
1) Tenemos que:  ........  (1)

Donde R es el circunradio del triángulo ABC.

También:

  ,  y

Debido a que los círculos circunscritos de los triángulos BHC, AHC y AHB son congruentes con el círculo circunscrito al triángulo ABC.

Luego:

  ...........  (2)

Reemplazando en (1):

             QED.   

Teorema 3:

En un triángulo ABC, su incírculo (I, r) determina un triángulo tangencial interno de área S, igualmente los incírculos (I₁, r₁), (I₂, r₂), (I₃, r₃) de los triángulos IBC, AIC, BIA determinan triángulos tangenciales internos de áreas S₁, S₂, S₃ respectivas en cada triángulo (Ver Fig. 3). Demostrar que:

Donde R = circunradio del triángulo ABC, r_E = inradio del triángulo excentral de ABC.

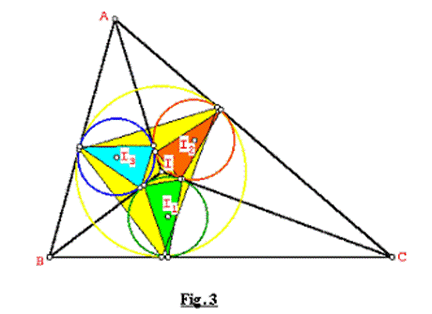
Demostración:   Ver Fig. 4

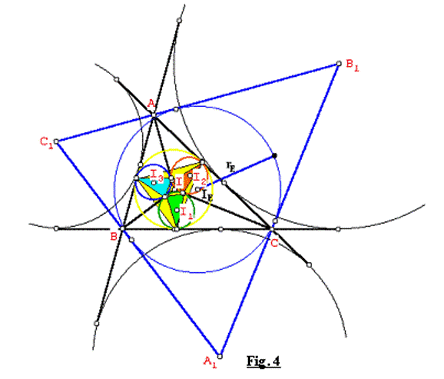
Consideramos el triángulo excentral A₁B₁C₁, cuyo incentro es I_E con inradio r_E.

Para el triángulo BIC, tenemos que: 

  .... (a)

Donde IA₁ es diámetro del círculo circunscrito al triángulo BIC y [XYZ] = área de XYZ.

También, como <BIC + <A₁ = 180º, entonces:

 

Donde: A₁B₁ = c₁, B₁C₁= a₁, C₁A₁= b₁

Además:, luego:

Reemplazando en (a):

  ..........(1)

De forma similar:

  ..........(2)

  ..........(3)

Sumando (1), (2) y (3):

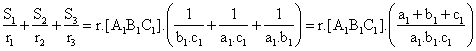
Pero:

Donde R_E = circunradio del triángulo excentral A₁B₁C₁, también R_E = 2R.

Reduciendo:

Pero también se cumple que el triángulo tangencial interno de ABC y el triángulo excentral A₁B₁C₁ son homotéticos (semejantes), luego: [A₁B₁C₁]/S = r_E²/r² y también: [ABC]² = S.[A₁B₁C₁],  por lo tanto:

, como R_E = 2R.

Finalmente:

                 QED.

Teorema 4:

Sea el triángulo acutángulo ABC, cuyo ortocentro es H y alturas son AA₀, BB₀, CC₀. Los círculos inscritos (I, r), (I₁, r₁), (I₂, r₂), (I₃, r₃), (H, r₀) correspondientes a los triángulos ABC, AB₀C₀, A₀BC₀,  A₀B₀C y A₀B₀C₀, determinan los triángulos tangenciales  internos de áreas S, S₁, S₂, S₃, S₀ correspondientes.

Demostrar que: 

1)  , donde R = circunradio de ABC.

2)

Demostración: Ver Fig. 5.

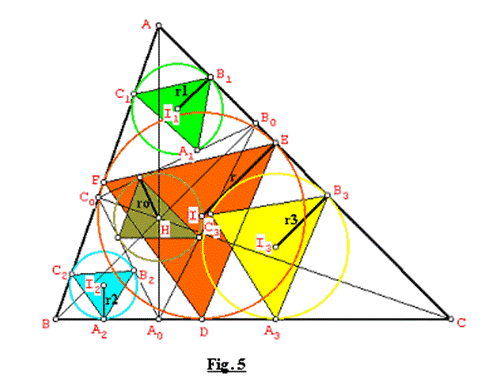
1) Tenemos que:  ........  (1)

Donde R es el circunradio del triángulo ABC.

También:

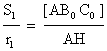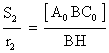  ,  y

Debido a que los círculos circunscritos de los triángulos AB₀C₀, A₀BC₀,  A₀B₀C son semejantes con el triángulo ABC, tenemos que:

Luego:

 

Entonces:

Pero por el teorema de Carnot: AH + BH + CH =2(r +R), luego:

  .........(2)

De (1) y (2):

             QED.   

2) Sabemos que:    ............ (1)

Debido a que el circunradio de DEF es .

Además por el teorema de Gergonne-Anne:

 

Entonces reemplazando en (1):

Luego:

, pero  como:

Por lo tanto:

Finalmente:

                   QED.

Teorema 5:

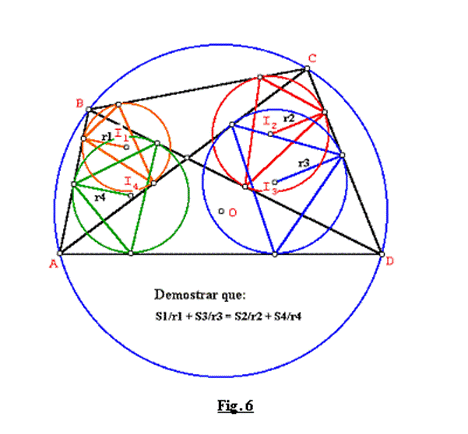
Sea el cuadrilátero ABCD inscrito en un círculo. Los círculos inscritos (I₁,r₁), (I₂,r₂),  (I₃,r₃), (I₄,r₄)  en los triángulos ABC, BCD, CDA y DAB, determinan los triángulos tangenciales internos de áreas S₁, S₂, S₃ y S₄ respectivamente.

Demostrar que:   

Demostración: Ver Fig. 6.

Sabemos que:   

Donde R es el circunradio de ABC (también de ABCD) y [XYZ] = Area de XYZ.

También:   

Entonces:

   .......... (1)

Similarmente:

   .......... (2)

Por lo tanto:

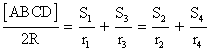           QED.   

Teorema 6:

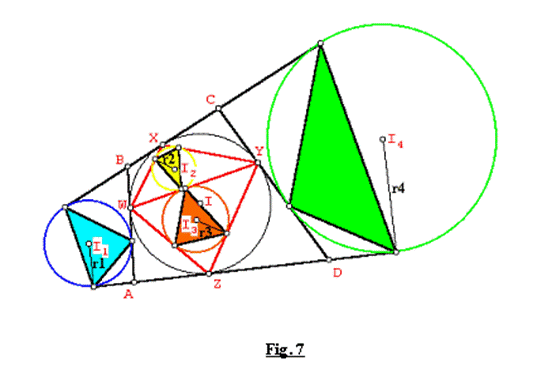
Sea el cuadrilátero ABCD circunscrito a un círculo (I, r). Los círculos exinscritos (I₁,r₁), (I₄,r₄)  correspondientes a los lados AB y CD y los círculos inscritos (I₂,r₂),  (I₃,r₃)  en los triángulos WXY y WYZ respectivamente, determinan los triángulos tangenciales  externos e internos de áreas S₁ , S₂, S₃ y S₄  correspondientes. Donde W, X, Y, Z son los puntos de tangencia del incírculo de ABCD sobre los lados AB, BC, CD, DA respectivamente.

Demostrar que:   

Demostración: Ver Fig. 7.

Sabemos que en un triángulo las áreas de su triángulo tangencial interno y externo son proporcionales a sus respectivos radios de los círculos que los determinan, en este caso tomando en cuenta de acuerdo a la configuración, que al prolongar los lados BC y AD se intersecan en un punto que lo denominaremos P (no trazado en la figura), tenemos que:

 

 Donde r es el circunradio de XWZ (inradio de ABCD) y  [XWZ] = Area de XWZ.

También:

 

Luego:

  ...........  (1)

Además en el triángulo XYW, las áreas del triángulo tangencial interno y del triángulo cumplen la relación:

 

También de manera similar, en el triángulo WYZ:

 

Entonces:

 .............(2)

Por lo tanto de (1) y (2):

             QED.   

Teorema 7:

Sea el cuadrilátero ABCD bicéntrico  de incírculo (I, r), con círculos exinscritos (I₁,r₁), (I₂,r₂) correspondientes a los lados AB y CD. Donde W, X, Y, Z son los puntos de tangencia del incírculo de ABCD sobre los lados AB, BC, CD, DA respectivamente.

Los círculos exinscritos I₁ e I₂ determinan los triángulos tangenciales  externos de áreas S₁, S₂ correspondientes. Si [WXYZ]  = Area de WXYZ.

Demostrar que:

1)   

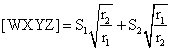
2)

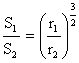
Demostración: Ver Fig. 8.

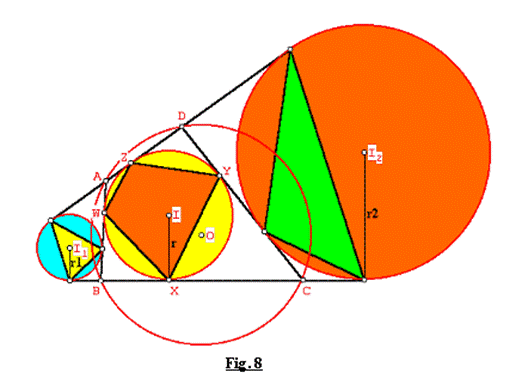
1) Tenemos que:

 , Donde r es el circunradio de XWZ (inradio de ABCD).

También: 

Luego:

  ...........  (1)

También, como el cuadrilátero ABCD es bicéntrico: r² = r₁.r₂

Reemplazando en (1):

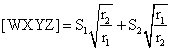             QED.    

2) Las  prolongaciones de AD y BC, según la configuración, se cortan en P, no trazado en la figura, luego tenemos que los triángulos PAB y PCD son semejantes, entonces:

  y   , ya que sus triángulos tangenciales son semejantes también.

Entonces:

 

Donde: r² = r₁.r₂, luego:

  ..................(1)

Por el resultado previo en la parte 1):

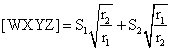 .............. (2)

De (1) y (2):

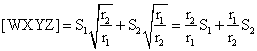
Finalmente:

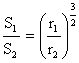               QED.

Referencias:

[1] J.C. Salazar, Algunos Teoremas y sus Demostraciones, Revista Escolar de las Olimpiadas Iberoamericanas Nº 13, Pág. 7:

http://www.campus-oei.org/oim/revistaoim/numero13.htm

Juan Carlos Salazar

caisersal@yahoo.com