Problema 208.
Un triángulo equilátero inscrito.
Bryant, V.W. y Austin, A.K. (1983): Reading in Mathematical Education. Geometry.
Seleccionado por Marion Walter. Association of Teachers of Mathematics.
Los profesores Bryant y Austin estaban en la Universidad de Scheffield
Traducción de Ricardo Barroso Campos.(Didáctica de las Matemáticas) Universidad de Sevilla.
Recientemente hemos propuesto la siguiente cuestión en una clase de jóvenes matemáticos:
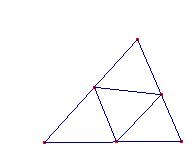
| "Dado un triángulo, mostrar cómo se construyen tres puntos, uno en cada lado, de manera que formen los vértices de un triángulo equilátero." |
Esta situación se ilustra así:

Trataremos una variedad de soluciones elegantes, y con una generalización importante de los resultados, de las que presentaremos algunas de las posibles soluciones. En primer lugar señalemos que los tres puntos se pueden construir de forma que no es única:
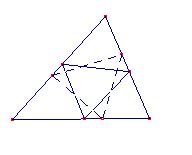
También en algunos casos es necesario elegir un punto de partida para alguna de estas construcciones. Como dijo un miembro de la clase: "¡El primer punto se eleige "de manera sensible"!, y asumimos que siempre es este el caso. De hecho esto signifca excluir unos puntos que no son sensibles.
Ejemplo 1.- (i) Escogemos A' en AB y consturimos D en BC tal que <DA'B = 30º.
(ii) Construimos la mediatriz de A'D que cortará a AC en E.
(iii) Construimos la circunferencia de centro E y radio ED que cortará a AB en A' y F.
Entonces DEF es triángulo equilátero.
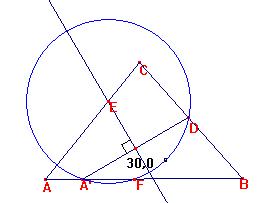
(Razones: Por las propiedades de una circunferencia, es <FED=2 <FA'D=60º. Además, dado que EF=ED, se sigue que DEF es equilátero)
Ejemplo 2.
(i) y (ii) como en el ejemplo 1.
Construimos la mediatriz de DE. Cortará a AB en F.
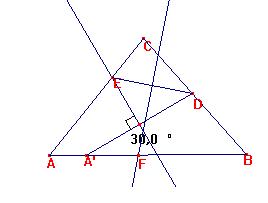
DEF es el mismo triángulo equilátero del ejemplo1.
Ejemplo 3
(i) Elegimos D en BC tal que AD sea la bisectriz de <BAC.
(ii) Construimos E en AB y F en AC tal que <EDA=<FDA=30º.
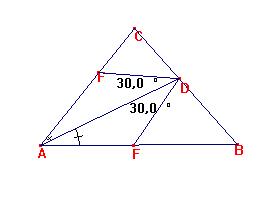
Entonces DEF es triángulo equilátero.
(Razones: Claramente los triángulos DEA DFA son congurentes, de donde DE=DF y DEF es triángulo equilátero).
Ejemplo 4
En este ejemplo construimos un triángulo equilátero inscrito con nuevas restricciones de manera que uno de sus lados sea paralelo a BC.
(i) Construimos un triángulo equilátero BCX como se muestra.
(ii) Construimos una recta a través de X, paralela a BC, que al cortar a AB da lugar al punto Y , y al cortar a AC da lugar al punto Z.
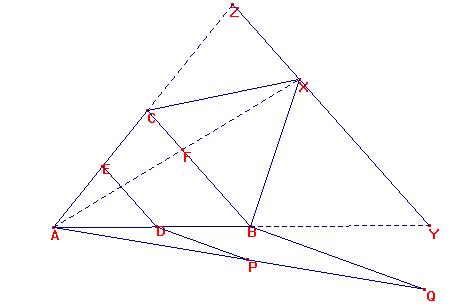
(iii) Construimos una recta APQ tal que <YAQ sea agudo, y AP = AB y AQ = AY
(iv) Construimos D en AB tal que PD//QB , E en AC tal que DE//BC, y sea F el punto de encuentro a BC y AX.
Entonces DEF es un triángulo equilátero.
(Razones: DEF está inscrito en ABC es una versión "a escala" de BCX inscrito en AYZ)
Ejemplo 5.
(i) Escojamos cualquier A' en AB y constuyamos D en AC y E en BC con:
<DA'A = <EA'B=60º.
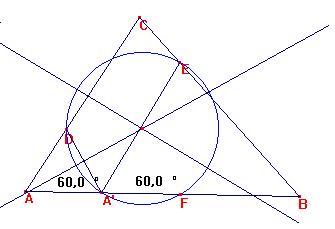
(ii) Construyamos la circunferencia a través de D E y A'. Cortará otra vez a AB en F.
Entonces DEF es un triángulo equilátero.
(Razones: Por las propiedades de la circunferencia,
<DFE = < DAE =60º, y <FDE =< FA'E=60º)
Finalmente damos una generalización sorprendente de la contrucción anterior:
Problema:
En la situación geométrica expuesta (con una descripción analítica que puede ser descrita,
cuya descripción gráfica se da) construir tres puntos , uno en a otro en b y otro en c,
de manera que formen un triángulo equilátero.
Soluciones.
Podemos adaptar los ejemplos 1 2 y 5 para este problema más general.
Por ejemplo como se ha hecho en 5, escojamos P en c, y construyamos D y E
como se muestra.
Entonces la circunferencia que pasa por D, E y P, encuentra a c otra vez en F.
El triángulo DEF es equilátero..
Es sorprendente cuánta diversión guarda el "eterno triángulo".