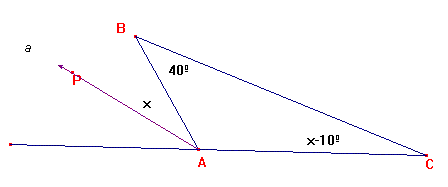
Problema 191 Para el aula

Ejemplo 2

En un triángulo ABC, tomemos P tal que B y P estén en el mismo semiplano respecto a la recta AB y tal que AP sea bisectriz exterior del ángulo en A.

Sean <PAB=x, <BCA=x-10º, y <ABC=40º.

Calcular las mdeidas de los ángulos < A, <C y el exterior de A del triángulo.

Rojo, A., Sánchez S.C., Greco, M.(1973). Matemática 1. Editorial El Ateneo. Buenos Aires. (página 246).

(adaptación del problema, que en su versión original es:

En el siguiente gráfico, AP(vector) es la bisectriz del ángulo exterior a del ABC (triángulo)

Gráfico modificado

Calcularemos las medidas de A , C y a )

Loa autores eran: Armando O. Rojo, Titular en el Instituto Superior del Profesorado y en el

Colegio Nacional de Buenos Aires, Silvia C. Sánchez,y Mario Greco, Titulares en el Colegio Nacional de Buenos Aires)

 Solución de Maite Peña Alcaraz, estudiante de Industriales en la Universidad de Comillas (Madrid)(15 de setiembre de 2004):

Por ser AP la bisectriz del ángulo exterior, AP es perpendicular a la bisectriz, así que x=90º-A/2. C=x-10º=90º-A/2-10º=80º-A/2. B=40º y sabiendo que A+B+C=180º se obtiene que A+ 40 +80 –A/2 = A/2 +120 =180 , luego A=120, x= 30 así que C=30-10 =20 y el ángulo externo a=180-120=60.