Problema 192.-
Supongamos que el punto P se encuentra sobre la circunferencia K descrita alrededor del triángulo ABC y que P₁ P₂ y P₃ son los puntos simétricos con el punto P respecto a los lados del triángulo ABC.
Demostrar que los puntos P₁, P₂ y P₃ están sobre una recta que pasa por el punto de intersección de las alturas del triángulo ABC.

Lyúbich, Y.I., Shor, L.A. (1976, original ruso, 1978 edición en español).
Método cinemático en problemas geométricos. Lecciones populares de Matemáticas.
Editorial Mir. Moscú. (traducción de Lozhkin, G.A.). (pág 51)

Solución de F. Damián Aranda Ballesteros, profesor del IES Blas Infante de Córdoba.
Estableceremos la demostración basándonos en los siguientes dos resultados:

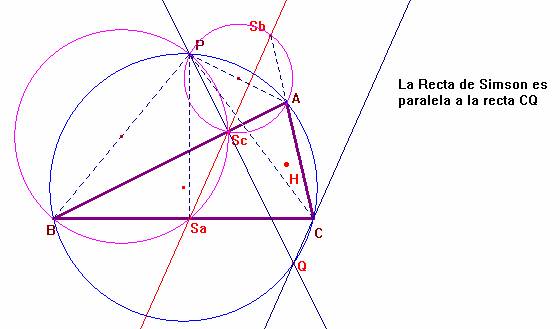
Lema 1.- La recta de Simson es paralela a la recta CQ.

Dem.- Sea Q el segundo punto de intersección de la recta PSc con la circunferencia K.

A partir de la circunferencia circunscrita PS_cAS_b, obtenemos la igualdad:
            <PS_cS_b = <PAS_b

Por otra parte, <PAS_b = 180º - <PAC = <PBC = <PQC.

De este modo, <PS_cS_b = <PQC y así, el segmento S_bS_c es paralelo a la recta CQ.

Procediendo de igual manera a partir de la circunferencia circunscrita PS_cS_aB, obtendríamos que el segmento S_cS_a sería también paralelo a la recta CQ.

En definitiva, los puntos S_a, S_b y S_c están alineados (Recta de Simson) y ésta es paralela a la recta CQ, c.q.d.

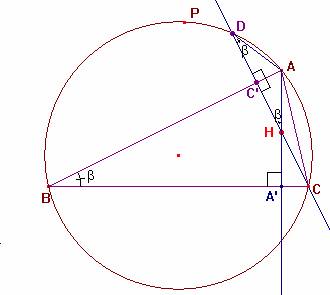
Lema 2.- La recta de Simson correspondiente al punto P divide por la mitad al segmento PH, donde  H es el ortocentro del triángulo ABC.

Dem.- Sea C' el pie de la altura correspondiente al vértice C. Si prolongamos esta altura hasta cortar de nuevo a la circunferencia K, obtenemos el punto D.
Conocemos el resultado C'H = C'D.

Para "ver" esto más evidente, basta observar las igualdades entre los ángulos siguientes: <ABC = <ADC' En el triángulo rectángulo AA'B, el ángulo <C'AA'= <C'AH es el complementario al ángulo <ABC. Por ello, los triángulos AC'H y AC'D además de semejantes, son iguales. En concreto, C'D = C'H

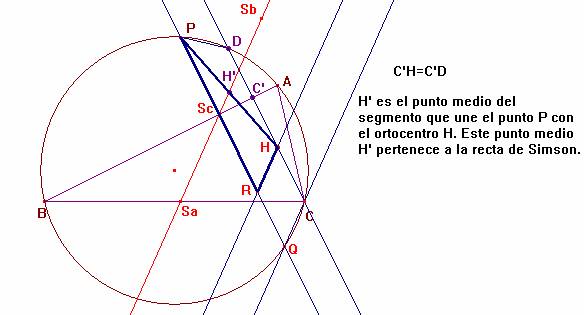
Las rectas PQ y CD son paralelas (ambas son perpendiculares al lado AB). Por tanto, al trapecio PQCD es isósceles. Por el punto H trazamos la paralela a la recta CQ, que será (Lema 1) también paralela a la recta de Simson. De esta manera obtenemos otro trapecio isósceles, el PRHD. Como tenemos que C'H=C'D, el punto C' es el punto medio de la base HD y así también el punto S_c lo será del lado PR, ya que C'S_c es perpendicular al lado AB.

En el triángulo PHR, la recta de Simson, S_aS_bS_c es la paralela media al lado HR, y así H' es el punto medio del segmento PH, c.q.d.

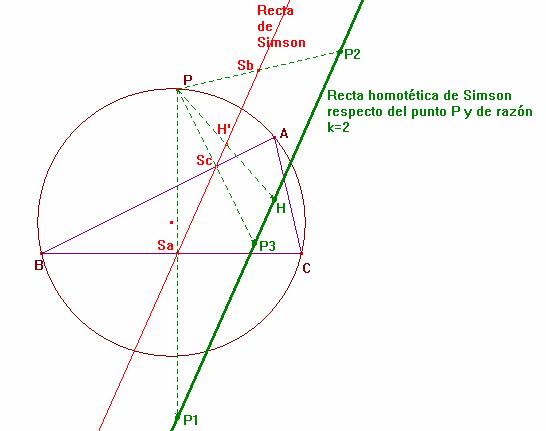
Proposición.- Los puntos P₁, P₂ y P₃ están sobre una recta que pasa por el punto de intersección de las alturas del triángulo ABC.

Solución.- La proposición anterior es consecuencia directa de los anteriores lemas, si tenemos en cuenta que P₁, P₂ y P₃ son los transformados de los puntos S_a, S_b y S_c por la homotecia de centro el punto P y de razón k=2. En esta homotecia, el punto H' se transformará en H, ortocentro del triángulo ABC.

En definitiva, los puntos P₁, P₂ y P₃ se encuentran sobre la recta paralela a la de Simson que pasa por el punto H, ortocentro del triángulo ABC.