Problema 192.-

10. Supongamos que el punto P se encuentra sobre la circunferencia K descrita alrededor del triángulo ABC y que P1 P2 y P3 son los puntos simétricos con el punto P respecto a los lados del triángulo ABC. Demostrar que los puntos P1 P2 y P3 están sobre una recta que pasa por el punto de intersección de las alturas del triángulo ABC.

Lyúbich, Y.I., Shor, L.A. (1976, original ruso, 1978 edición en español. ). Método cinemático en problemas geométricos. Lecciones populares de matemáticas. Editorial Mir. Moscú. (traducción de Lozhkin, G.A.). (pág 51)

 Solución de Maite Peña Alcaraz, estudiante de Industriales en la Universidad de Comillas (Madrid) (15 de setiembre de 2004):

Sean P´1, P´2 y P´3 las proyecciones de P sobre los lados del triángulo ABC. P´1, P´2 y P´3 están alineados por propiedades de la recta de Simson. Una homotecia de centro P y radio 2 transforma estos tres puntos en P1, P2 y P3 que por tanto también estarán alineados.

Ahora si le damos coordenadas a los puntos:

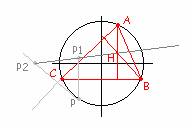
Colocando en el centro de la circunferencia circunscrita a ABC el origen de coordenadas y considerando BC paralela al eje de las x, tenemos que las coordenadas de los puntos son:

 P2 es también fácil de calcular, sabiendo que el vector director perpendicular a la recta AC es y que se hace la perpendicular desde P, y P2 es el simétrico de P respecto de . Por tanto tenemos que:

 Y por último para comprobar que los tres puntos están alineados basta comprobar que los vectores directores P2P1 y P1H son proporcionales. Si se multiplica P2P1 para quitarle el denominador se ve fácilmente que sí lo son y por tanto que H está contenido en la recta P1P2P3.