Problema 192.- 10. Supongamos que el punto P se encuentra sobre la circunferencia K descrita alrededor del triángulo ABC y que P₁ P₂ y P₃ son los puntos simétricos con el punto P respecto a los lados del triángulo ABC. Demostrar que los puntos P₁ P₂ y P₃ están sobre una recta que pasa por el 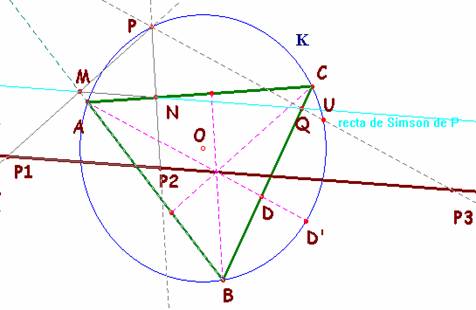punto de intersección de las alturas del triángulo ABC.

Lyúbich, Y.I., Shor, L.A. (1976, original ruso, 1978 edición en español. ). Método cinemático en problemas geométricos. Lecciones populares de matemáticas. Editorial Mir. Moscú. (traducción de Lozhkin, G.A.). (pág 51)

Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca..- Si son M, N y Q los pies de las perpendiculares desde P a los lados del triángulo ABC, resultará que los triángulos PMN y PP₁P₂ son semejantes por tener un ángulo común (el ángulo en P) y los dos lados proporcionales, por tanto el tercer lado P₁P₂ es paralelo a MN. El mismo razonamiento con los otros puntos P_i nos conduce a la alineación de los mismos en una recta, que es paralela a la recta de Simson de P.

Para probar que esta recta contiene al ortocentro H del triángulo procedemos como sigue:

Como el segmento HD es igual al DD’(ver problema nº 166), resulta que el triángulo HRD’ es isósceles, y también su homotético el triángulo VRP, con lo cual QV = PQ, es decir el punto V es el punto P₃.

Como < UAD’ <UPD’= <VHD’, resulta que las rectas HV y AU son paralelas. Probando finalmente que la recta AU es paralela a la recta de Simson de P habremos concluido la demostración.

En el cuadrilátero inscriptible PCQN obtenemos <PCN = <PQN. De otra parte, <PUA =< PCA =<PCN = <PQN, que significa que AU y la recta de Simson son paralelas pues forman el mismo ángulo con la recta PV. Y con esto concluimos.