Problema 193.-
Dado un triángulo ABC, hallar el lugar geométrico del ortocentro cuando A recorre la recta paralela al segmento BC.

Martel, J. (2001): Lugares geométricos relacionados con un triángulo cuyos vértices son puntos de una curva plana cualquiera. En Socas, M., Camacho, M, Morales, A. (Eds). Formación del profesorado e investigación en educación matemática III. Didáctica de las Matemáticas. Departamento de Análisis Matemático. Universidad de La Laguna. (154)

Solución de F. Damián Aranda Ballesteros, profesor del IES Blas Infante de Córdoba.

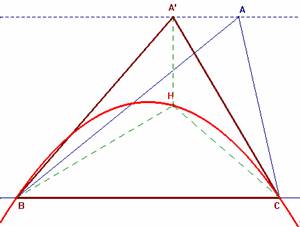
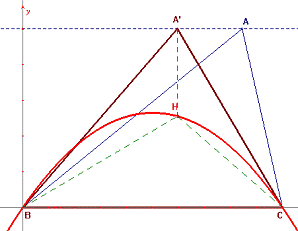
Dado el triángulo ABC, consideramos el sistema de referencia que determinan el punto B como origen y los lados BC como eje x y su perpendicular por B, como eje y. De esta manera, los anteriores elementos tendrán las siguientes coordenadas y ecuaciones según corresponda: * Puntos: A'(a, k) k¹0, B(0,0) y C(a,0) * Rectas: A'C º k×x-(a-a)×y= k×a; BC º y= 0; Altura ha' º x=a; Altura hbº (a-a)×x +k×y = 0; * Punto H (ortocentro del triángulo A'BC): Eliminando el parámetro a de las coordenadas del punto H, obtenemos la ecuación del L.G. solicitado: 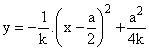, 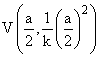de vértice , que corresponde a la ecuación de una parábola. Observamos que el lado BC es una cuerda de dicha parábola.