Problema 193

Dado un triángulo ABC, hallar el lugar geométrico del ortocentro cuando A recorre la recta paralela al segmento BC.

Martel, J. (2001): Lugares geométricos relacionados con un triángulo cuyos vértices son puntos de una curva plana cualquiera. En Socas, M., Camacho, M, Morales, A. (Eds). Formación del profesorado e investigación en educación matemática III. Didáctica de las Matemáticas. Departamento de Análisis Matemático. Universidad de La Laguna. (154)

Con permiso de su autor, a quien el director/editor agradece su atención.  

SoluciónMaite Peña Alcaraz, estudiante de Industriales en la Universidad de Comillas (Madrid). (30/9/2004):

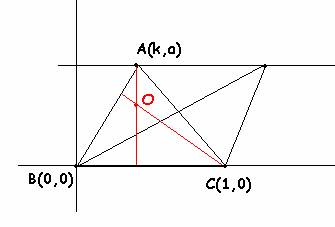
Tomemos el triángulo ABC en los ejes de coordenadas. La altura H_A es x=k, mientras que la altura H_B tiene como vector director el perpendicular a (k-1,a), esto es (-a,k-1) y por vértice el punto B(0,0), es decir, es la recta (k-1)x+ay=0.

El ortocentro O que es la intersección de estas rectas tiene por coordenadas, x=k, y=(k-1)k/a, es decir es una parábola y=x²/a-x/a siendo x la componente x del punto A.