Problema 195.- (Para el aula)
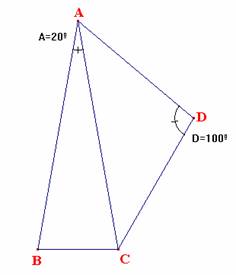
La figura que se adjunta está formada por dos triángulos isósceles, con el ángulo en A de 20º yel de D de 100º. Demostrar que AB = BC + CD.
Giornalino del grupo Tutor.
Solución de F. Damián Aranda Ballesteros, profesor del IES Blas Infante de Córdoba.
|
|
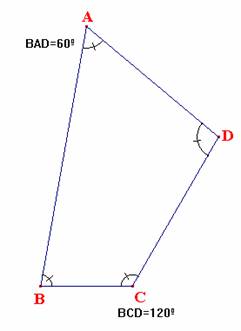
lo cual indica que el cuadrilátero ABCD es cíclico. |
|
|
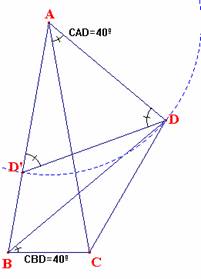
Si trasladamos el lado AD sobre el lado AB obtenemos el punto D'. Por otro lado, tenemos la siguiente igualdad entre ángulos, <CBD= <CAD= 40º. En conclusión: AB= AD' + D'B AB= CD + BC, c.q.d. |