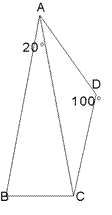
La
figura qui riportata è formata da due triangoli isosceli, uno con l'angolo
al vertice (in A) di 20º, l'altro (in D) di 100º. Provare chePara el aula.
La
figura qui riportata è formata da due triangoli isosceli, uno con l'angolo
al vertice (in A) di 20º, l'altro (in D) di 100º. Provare che
AB=BC+DC
Solución de Francisco Javier García Capitán
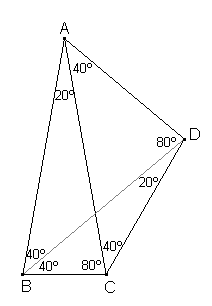
Completando los ángulos de los triángulos isósceles observamos que los ángulos B(=80º) y D(=100º) del cuadrilátero ABCD suman 180º, por lo que este cuadrilátero está inscrito en una circunferencia.
 |
 |
|
Fig. 1
|
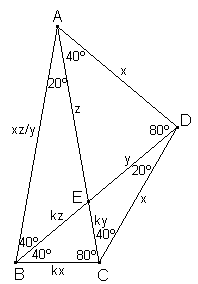
Fig. 2
|
Como los ángulos inscritos que abarcan el mismo arco miden lo mismo, podemos completar los ángulos que intervienen en la figura 1.
Llamando x, y, z a los lados del triángulo EAD, y teniendo en cuenta los triángulos semejantes EAD y EBC por un lado y los triángulos semejantes CDE y BAE por otro podemos expresar las longitudes de todos los segmentos como en la figura 2.
Imponiendo que AB=AC y que BAE es semejante a BDC obtenemos las relaciones:
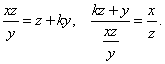
de donde es posible despejar
Entonces la condición AB = BC + DC se expresa
y sustituyendo el valor de x despejado arriba, la condición se reduce a
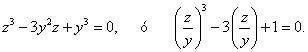
Si aplicamos el teorema de los senos al triángulo ADE,
resulta que 
por lo que lo único que queda es comprobar la validez de la fórmula
Para ello,
sólo tenemos que sustituir 
en
la identidad 