Problema 196.-
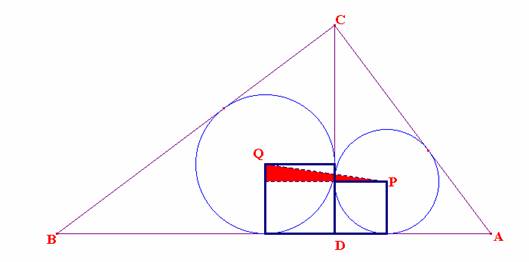
En el triángulo ABC, recto en C, sea CD una altura.

Los círculos de centros P y Q están inscritos en los triángulos ACD y BCD, respectivamente.

Si AC =15 y BC = 20, determine la medida de PQ.

Propuesto en la Olimpiada de Costa Rica.

Propuesto por Ricard Peiró i Estruch, profesor de Matemáticas del IES 1 de Xest (Valencia).

Solución de F. Damián Aranda Ballesteros, profesor del IES Blas Infante de Córdoba.

(1)   Por el teorema de Pitágoras, AB2 = AC2 + BC2;                AB = 25

(2)   Por el teorema del cateto, BC2 = AB× BD;                         BD = 16

(3)   Como AB = BD + DA, entonces                                          AD = 9

(4)   Por el teorema de la altura, CD2 =BD×DA;                        CD = 12

(5)   Hallamos el área del triángulo BCD;
S(BCD)= 1/2×BD×CD = 1/2×(BD + CD + AD )×r1, donde r1 es el radio del círculo de centro Q, inscrito en el triángulo BCD;                 
S(BCD)=1/2×16×12 = 1/2×(16+12+20)×r1;                              r1= 4

(6)   Hallamos ahora el área del triángulo ACD;
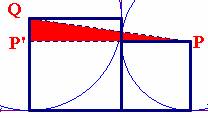
S(ACD)= 1/2×AD×CD = 1/2×(AD + CD + CA )×r2, donde r2 es el radio del círculo de centro P,  inscrito en el triángulo ACD;                 
S(ACD)=1/2×9×12 = 1/2×(9+12+15)×r2;                                  r2= 3

(7)   Del triángulo PP'Q, obtenemos que QP2 = PP'2 + P'Q2 ; QP2 = (r1+r2)2 + (r1-r2)2
QP2 = (4+3)2 + (4-3)2 ; QP2 =50 ; QP = 50;

(8)