Teniendo en cuenta los triángulos semejantes ABC, ACD y CBD, podemos expresar las medidas de los segmentos AD, CD y BD de la manera en que aparecen en la figura.
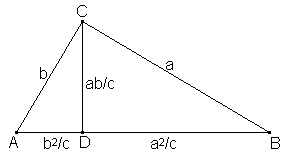
En el triángulo rectángulo ABC , recto en
C sea CD una altura.
Los círculos de centros P y Q están inscritos en los triángulos
ACD y BCD respectivamente.
Si AC =15 y BC =20 determine la medida de PQ .
Propuesto por Ricard Peiró i Estruch Profesor de Matemáticas
del IES 1 de Xest (València)
Solución de Francisco Javier García Capitán
|
Teniendo en cuenta los triángulos semejantes ABC, ACD y CBD, podemos expresar las medidas de los segmentos AD, CD y BD de la manera en que aparecen en la figura. |
 |
|
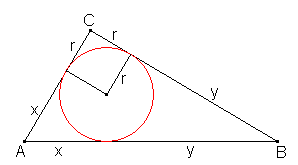
Usando esta otra figura, podemos expresar con facilidad el radio de la circunferencia inscrita en un triángulo rectángulo:
|
 |
|
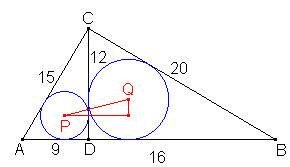
Con los datos AC=15 y BC=20, las medidas de todos los segmentos quedan determinadas y, usando la fórmula anterior para el radio de una circunferencia inscrita en un triángulo rectángulo, obtenemos que los radios de las circunferencias ACD y BCD son 3 y 4 respectivamente. Ahora basta usar el teorema de Pitágoras con el triángulito rojo para obtener que
|
 |