Propuesto por Ricard Peiró i Estruch Profesor de Matemáti cas del IES 1 de Xest (València)

Problema 196

En el triángulo rectángulo ABC , recto en C sea CD una altura.

Los círculos de centros P y Q están inscritos en los triángulos ACD y BCD respectivamente.

Si AC =15 y BC =20 determine la medida de PQ .

Propuesto en la Olimpiada de Costa Rica

Propuesto por Ricard Peiró i Estruch Profesor de Matemáti cas del IES 1 de Xest (València) (en catalán)

En un triangle rectangle ABC , C=90º, siga h= CD l'altura sobre la hipotenusa.

Els cercles de centre P i Q estan inscrits en els triangles ACD i BCD respectivament.

Si AC =15 , BC=20, determineu PQ.

Proposat en la Olimpíada de Costa Rica.

Solución de Maite Peña Alcaraz Estudiante de Industriales en la Universidad de Comillas (Madrid)

:

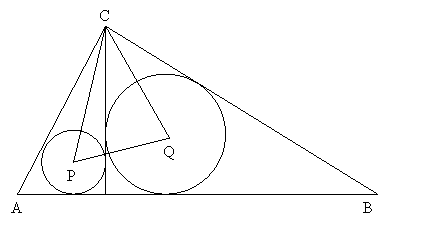
Tomemos el triángulo tal

como indica la figura.

Como AC=15, y BC=20, por el teorema de Pitágoras se puede obtener que AB=25 y usando entonces sen ABC=15/25 y sen BAC=20/25 podemos obtener ABC=36,87º y BAC=53,13º.

Trabajemos ahora con los triángulos APC y BQC para obtener las medidas CP y CQ. ACP=ACC´/2=ABC/2=QBC y QCB=C´CB/2=BAC/2=PAC.

Por tanto podemos calcular que APC=BQC=135º y po r el teorema del seno en cada uno de los dos triángulos obtenemos que CP=9.49 y BP=8.94.

Por último, sabiendo que PCQ=45º=ACC´/2+BCC´/2=(ACC´+BCC`)/2=90º/2, usando el teorema del coseno con el triángulo CPQ obtenemos que PQ²=CP²+CQ²-2 CP CQ cos 45º, y operando PQ=7,07