Problema 196.-
En el triángulo rectángulo ABC , recto en C sea CD una altura.
Los círculos de centros P y Q están inscritos en los triángulos ACD y BCD respectivamente.
Si AC =15 y BC =20 determine la medida de PQ .
Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca.-
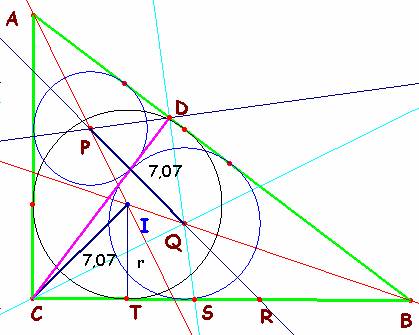
En la figura podemos ver que los triángulos CDQ, APD y AIC son semejantes: tienen sus tres ángulos iguales. De la semejanza de los dos primeros se deduce que 
, que prueba que PDQ es un triángulo rectángulo en D (PD y DQ son bisectrices) semejante a los otros que se forman al trazar la altura sobre la hipotenusa (PQD =b = CBA; DPQ = a =BAC).
De la semejanza con ADC obtenemos 
y de la semejanza de AIC con CQD, 
.
El producto de estas dos expresiones nos da PQ = CI.
Además, estos segmentos son perpendiculares.
Observemos el triángulo QSR. Un cálculo inmediato da que el ángulo S (DSB) mide 135 ─ b y como el ángulo Q mide b, necesariamente el ángulo R mide 45º, lo cual prueba la perpendicularidad.
La medida de PQ = CI es 
r, como puede fácilmente deducirse de la figura. El radio r de la circunferencia inscrita se calcula de la expresión del área del triángulo:
Área (ACB) = semiperímetro · radio circ. inscrita, esto es, 2pr = ab ð CI = PQ = 
r =
.
En este caso a= 20; b= 15; c = 25; 2p=60. ð r = 5 y CI = PQ = 5≈7,071.
Nota.- En la figura se ha tomado como unidad