Problema 196
En el triángulo
rectángulo ABC , recto en C sea
CD una altura.
Los círculos de
centros P y Q están inscritos en los triángulos ACD
y BCD respectivamente.
Si AC =15
y BC =20 determine la medida de PQ .
Solución de William Rodríguez Chamache. profesor de geometria de la "Academia integral class" Trujillo- Perú
1) por relaciones métricas obtenemos las siguientes medidas
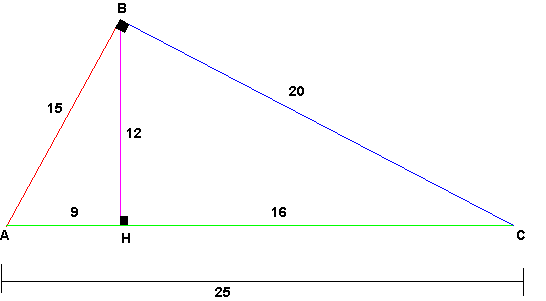
2) En los triángulos rectángulos AHB y BHC aplicamos el teorema de poncelet para calcular los radios r1 y r2
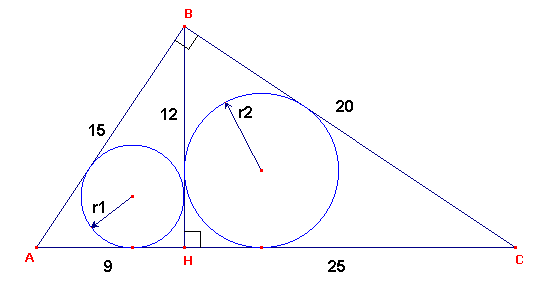
En triángulo ABH: 12+9=15+2(r1)…….. r1= 3
En triángulo BHC: 12+16= 20+2(r2)………r2=4
3) Aprovechando los puntos de tangencia obtenemos la gráfica siguiente
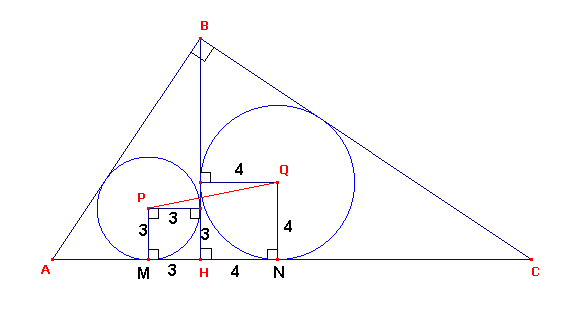
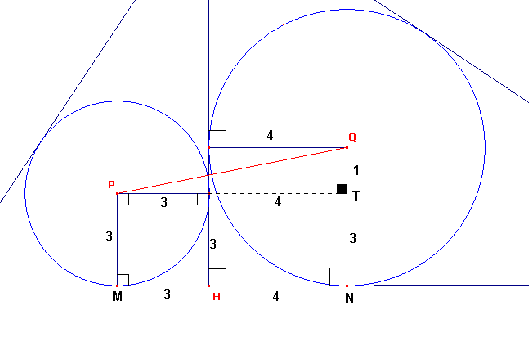
4) Finalmente en la siguiente gráfica en el triángulo PQT aplicamos el teorema de Pitágoras para obtener PQ: PQ2=72+12
Finalmente: PQ = ![]()