PROBLEMA 197:

En un triángulo rectángulo la diferencia de dos ángulos agudos es igual al ángulo comprendido entre la altura y la mediana relativa a la hipoenusa.

Solución de:

Profa. Mariela Lilibeth Herrera

Cursante de la Maestría en Enseñanza de la Matemática en la UPEL – Maracay - Venezuela

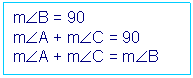
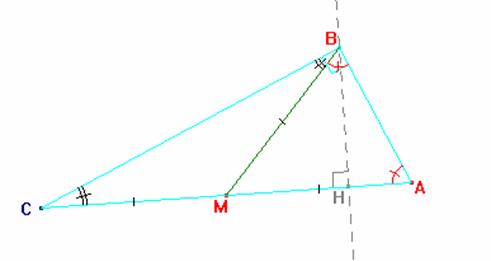Demostración: Sea el triángulo rectángulo DABC, tal que el ángulo B es recto, luego el ángulo A y el ángulo C son complementarios por el corolario que expresa: “Los ángulos agudos de un triángulo rectángulo son complementarios”. De las afirmaciones anteriores se deduce que la medida del ángulo A mas la medida del ángulo C es igual a la medida del ángulo B.

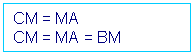Sea M el punto medio del segmento AC, es decir, M es el punto medio de la hipotenusa, y por definición de punto medio sabemos que: el segmento CM tiene igual longitud que el segmento MA. Así BM es la mediana del triángulo DABC con respecto a la hipotenusa, además el segmento BM también tiene la misma longitud que el segmento MA, esto es por el teorema: “La longitud de la mediana correspondiente a la hipotenusa de un triángulo rectángulo es la mitad de la longitud de la hipotenusa”

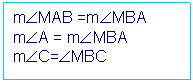El triángulo DAMB es isósceles, y por el teorema del triángulo isósceles:” Si dos lados de un triángulo son congruentes, entonces los ángulos opuestos a estos lados son congruentes”, afirmamos que los ángulos ÐMAB (ÐMAB=ÐA) y ÐMBA tienen igual medida. Análogamente, el ángulo ÐC y el ánguloÐ MBC son congruentes.

Por otro lado, consideremos la altura al triángulo DABC desde el vértice B, llamemos H al pie de la perpendicular, nótese que el punto H es un punto entre C y A, pues el pie de la altura coincidiría con uno de los vértices sólo si el ángulo asociado a dicho vértice fuera recto, pero los ángulos ÐA y ÐC son agudos, además el pie de la altura esta en la prolongación del lado cuando el triángulo posee un ángulo obtuso.

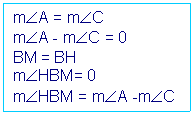Si el triángulo DABC es isorectángulo los ángulos ÐA y ÐC son congruentes, y la altura  y la mediana con respecto al vértice B coinciden, es decir, los segmentos BH y BM son sólo uno, por tanto, el ángulo ÐHBM es nulo, por tanto se cumple trivialmente que la medida del ángulo ÐHBM es la diferencia de las medidas de los ángulos agudos del triángulo rectángulo dado.

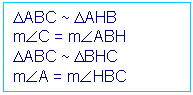En caso que el triángulo DABC no sea isósceles, se forma el triángulo rectángulo DAHB, con el ángulo de vértice H recto, y por el teorema que dice: “En un triángulo rectángulo cualquiera la altura correspondiente a la hipotenusa divide al triángulo en otros dos que son semejantes entre sí y semejantes también al triángulo original”, se garantiza que los triángulos  DABC, DAHB y DBHC son semejantes y por definición de semejanza los ángulos ÐABH y ÐC tienen igual medida, análogamente, ÐHBC y ÐA son ángulos congruentes.

Si la medida del ángulo ÐC es mayor que la medida del ángulo ÐA, entonces el punto H esta entre C y M, y el ángulo ÐCBM por el postulado de adición de ángulos es igual al ángulo ÐHBC mas el ángulo ÐHBM, luego la medida del ángulo ÐHBM es la diferencia de las medidas de los ángulos ÐCBM y ÐHBC, por tanto la medida del ángulo ÐC menos la medida del ángulo ÐA determina la medida del ángulo ÐHBM

Si la medida del ángulo ÐA es mayor que la medida del ángulo ÐC, entonces el punto H esta entre A y M, y el ángulo ÐABM es igual a la suma de los ángulos ÐHBA y ÐHBM, así el ángulo ÐHBM se obtiene como la diferencia de los ángulos ÐABM y ÐHBA, por tanto la diferencia del ángulo ÐA y del ángulo ÐC determina el ángulo ÐHBM.

En todos los casos la medida del ángulo formado por la mediana y la altura correspondientes al vértice del ángulo recto de un triángulo rectángulo dado, se obtiene a través de la diferencia de los ángulos agudos del triangulo original.