Problema 197

En un triángulo rectángulo la diferencia de dos ángulos agudos es igual al ángulo comprendido entre la altura y la mediana relativa a la hipotenusa.

Severi, F (1952): Elementos de geometría. I. Editorial Labor. Manuales Técnicos Labor. Francisco Severi de la Universidad de Roma y de la Academia de Italia. Con 222 figuras. Traducción de la Segunda edición italiana por el profesor T. Martín Escobar, de la Escuela Industrial de Gijón. Tomo Primero. Tercera Edición. Reimpresión. Editorial Labor, SA. Barcelona, Madrid, Buenos Aires, Río de Janeiro, México, Montevideo.

Bruño (1958): Geometría Curso superior. Madrid. p. 166 (Referencia ofrecida por el profesor Ricard Peiró i Estruch, a quien el director agradece su información)

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona)

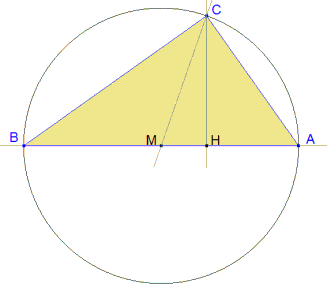
Por ser ABC rectángulo en C; A+B=π/2.

Por ser AHC rectángulo en H; A+∠HCA=π/2.

En el triángulo AMC; ∠MCA+A+∠AMC=π.

En el círculo el ángulo de cuerda AC es B; en el centro el ángulo es el doble; ∠AMC=2B;

∠MCH=∠MCA-∠HCA=(π-A-∠AMC)-(π/2-A)=π/2-∠AMC=(A+B)-2B=A-B