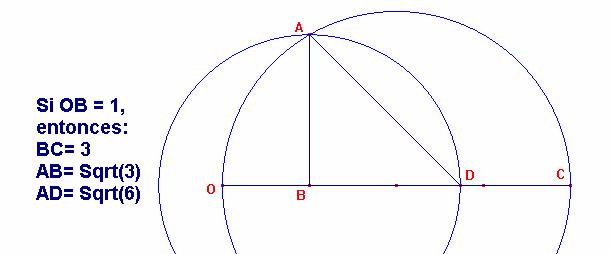
Problema 198    

Construir un triángulo rectángulo cuya hipotenusa mide 12 cm, sabiendo que dos de sus medianas son perpendiculares.

García Capitán, F (2004): Propuesta personal

Solución de F. Damián Aranda Ballesteros, profesor del IES Blas Infante de Córdoba.

Del análisis de la figura, observamos los siguientes hechos de interés:

1.- Las medianas relativas a los ángulos agudos del triángulo  rectángulo no pueden ser perpendiculares entre sí. Veamos esto con mayor detalle.

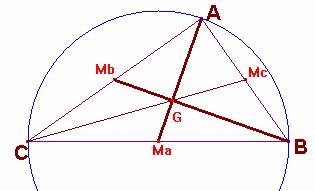
* Si m_b ^ m_c, el cuadrilátero AM_bGM_c sería cíclico con diámetro el valor:
 AG = 2/3×m_a = 2/3×1/2×BC = 4cm

* Por otra parte el triángulo medial AM_bM_c, semejante al triángulo inicial ABC, tendría como circunferencia circunscrita una de diámetro igual a: 1/2×12 = 6 cm

2.- Una de las dos medianas perpendiculares entre sí será la correspondiente al ángulo recto A, m_a. Será, pues la otra, m_b.

3.- De este modo, por el teorema de la altura, AG² = M_bG×GB.
Por tanto, si llamamos  AG= 2/3×6 = 4;             M_bG= x;         GB= 2x

obtenemos que:            ;             

4.- Ahora calculamos los lados AM_b y AB usando el teorema del cateto. En concreto, se tendrá que:            ;       

5.- En definitiva, los lados iniciales del triángulo ABC, rectángulo en A, son los siguientes:

5.- Dicho triángulo es semejante al de lados , cuya construcción no presenta ninguna dificultad.