Problema 198 de triánguloscabri

Construir un triángulo con hipotenusa 12, sabiendo que dos de sus medianas son perpendiculares.

Solución de Francisco Javier García Capitán

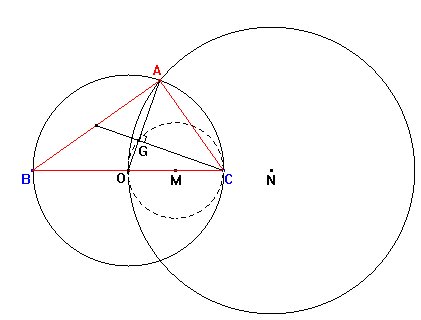
• Fijamos un segmento BC de longitud arbitraria. Llamamos O al punto medio de BC y G al baricentro del triángulo ABC buscado.
• En la figura observamos que desde el baricentro G se ve OC bajo un ángulo recto, por lo que G está en la circunferencia de diámetro OC. Llamamos M al centro de esta circunferencia.
• La distancia OG es la tercera parte de la distancia OA.
• Haciendo una homotecia de centro O y razón 3, el punto G irá a parar a donde ahora está el punto A, por lo que A está en una cirunferencia de centro N y radio 3·OM, siendo N el punto simétrico de M respecto de C.
• Por supuesto, A también está en la circunferencia de diámetro BC.
• Entonces, podemos hallar A como intersección de dos circunferencias.