| Problema 198 Construir un triángulo rectángulo cuya hipotenusa mide García Capitán, F (2004): Propuesta personal |
Solución:
Como tenemos un triángulo rectángulo las medianas perpendiculares no pueden ser las dos de dos catetos, sino que tiene que ser una mediana correspondiente a un cateto con la mediana correspondiente a la hipotenusa las que formen 90º.
En ese caso:
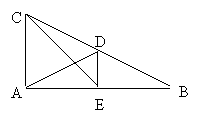 |
Si AD y CE son perpendiculares, DE es perpendicular a AB por el Teorema de Tales, ya que DEB es semejante a CAB.
Si llamamos b a DE, y c a EB, AB=2c, y CA=2b, así que el área de ABC será cuatro veces la de DEB.
Además DAE=DEB, ya que tienen un ángulo igual DEB=DEA=90º, y los lados que lo comprenden iguales DE=DE y AE=EB por ser E el punto medio de AB.
Por tanto DA=6cm=DB=DC. Por tanto ADC es un triángulo isósceles.
Si llamamos G a la intersección de DA y EC, DEG y AGE son semejantes también a ABC.
Además GD=2cm, ya que dos medianas se cortan en la proporción 2/3 y 1/3. Así que por el teorema de Tales entre los triángulos sabemos que DG/CA=DE/AB; es decir 2/2b=b/12 así que b2=12 y b es raíz de 12.
Por último para calcular AB basta usar el teorema de Pitágoras, y obtenemos que c es la raíz cuadrada de 24. Calcular la raíz de un segmento se puede hacer gráficamente usando el teorema de la altura, mn=h2 haciendo m=2 y n=12, una circunferencia con centro en el centro de la suma de los segmento m+n y levantando por el extremo de m una perpendicular a m+n y donde corta con la circunferencia obtenemos el segmento h de longitud raíz de 24.
Construir un triángulo rectángulo conocidas las medidas de la hipotenusa y un cateto, se puede hacer haciendo una circunferencia de diámetro la hipotenusa y en algún extremo de un diámetro hacer un arco de longitud del cateto, obteniéndose el vértice A. B y C son los extremos del diámetro.