Construir un triángulo con hipotenusa 12, sabiendo que dos de sus medianas son perpendiculares.

Solución de Martha Iglesias Inojosa. Profesora del Departamento de Matemática. Universidad Pedagógica Experimental Libertador (Maracay – Venezuela).  Domingo, 24 de Octubre de 2004.

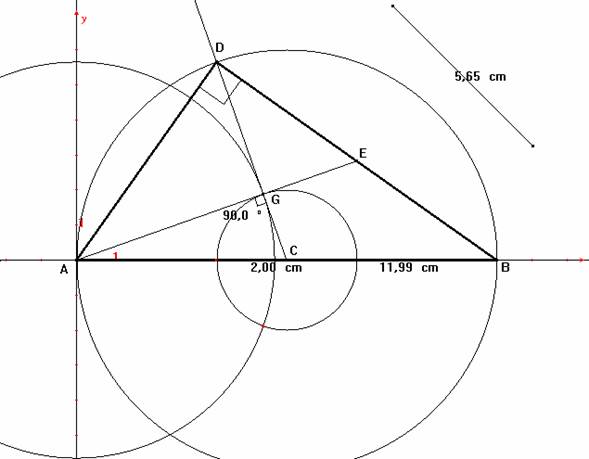
Sea AB la hipotenusa de un triángulo rectángulo ABD tal que AB = 12 cm. Sea C el punto medio de AB, de modo que AC = BC = 6 cm. Haciendo centro en C y con una abertura CA, se traza una circunferencia C1 que contendrá al vértice D del ángulo recto (aún sin localizar) del triángulo ABD. ¿Cómo hallar al punto D, de modo que dos medianas del triángulo sean perpendiculares?

Se conoce que DC será la mediana con respecto a la hipotenusa y, por ende, se cumplirá que DC = AB / 2 = 6 cm y, además, que GC = DC / 3 = 2 cm, siendo G el baricentro del triángulo ABD. Haciendo centro en C y con una abertura  de 2 cm, se traza una circunferencia C2. Para que la mediana DC sea perpendicular a la mediana AE, siendo E el punto medio del lado BD, el triángulo ACG debe ser rectángulo, con ángulo recto en G. Dado que AC = 6 cm y GC = 2 cm, el lado AG deberá medir 4Ö 2 cm. Haciendo centro en A y con una abertura de 4Ö 2 cm, se traza una circunferencia C3. Se busca el punto de intersección de las circunferencias C2 y C3, el cual será el baricentro del triángulo ABD. Se traza la semirrecta CG, la cual corta a la circunferencia C1 en el punto D.  Se construye el triángulo ABD. Se ubica el punto medio E del segmento BD y se traza la mediana AE.