Problema 198
Construir un triángulo rectángulo de hipotenusa 12 cm , sabiendo que dos de sus medianas son perpendiculares.
García Capitán, F (2004): Propuesta personal
Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona)
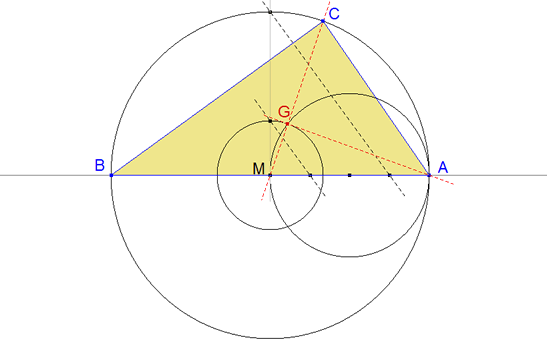
Dado un triángulo rectángulo ABC, rectángulo en C y sea M el punto medio de AB. (AB=12)
Si dos medianas son perpendiculares, significa que el baricentro, G, es vértice de un ángulo recto y por tanto si una de las medianas llega al punto medio de la hipotenusa y la otra mediana parte de uno de los vértices sobre dicha hipotenusa; podemos decir que el baricentro de este triángulo estará sobre un círculo de diámetro AM.
Sabemos que el baricentro está en el tercio de las medianas. Como el triángulo buscado es rectángulo, el vértice C estará sobre el círculo de diámetro AB y por tanto el baricentro estará sobre un círculo de radio AM/3.
El baricentro estará en la intersección del círculo de diámetro AM y el círculo de centro M y radio AM/3.
La intersección de la recta MG con el círculo de diámetro AB nos proporciona el vértice C.