Problema 198.- Construir un triángulo rectángulo cuya hipotenusa mide
Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca.
Las medianas que salen de los ángulos agudos no pueden ser perpendiculares, pues los ángulos agudos del triángulo BGC (menores que los de BAC) no suman 90º.
Trazamos las medianas desde los vértices A y C. Por tratarse de un triángulo rectángulo, AM = BM = radio del círculo circunscrito = a/2. De la propiedad del baricentro, AG = 2/3·AM = a/3; b=áng(ABC), g= áng(BAC). Las medianas trazadas definen dos triángulos isósceles, AMC y AMB. Comparando ángulos llegamos a 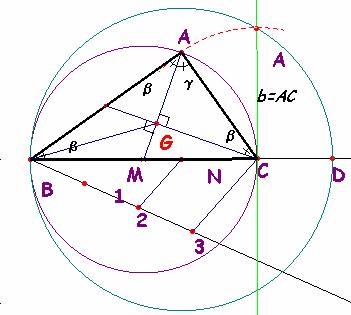 la semejanza de los triángulos rectángulos AGC y CAB . Esta semejanza implica que
la semejanza de los triángulos rectángulos AGC y CAB . Esta semejanza implica que ![]() , es decir, que el cateto b = AC es media proporcional entre la hipotenusa a y el segmento AG.
, es decir, que el cateto b = AC es media proporcional entre la hipotenusa a y el segmento AG.
La construcción se realiza como sigue: Se llevan sobre una semirrecta, uno a continuación de otro, los segmentos BC (hipotenusa) y AG. Con el segmento suma como diámetro se traza una circunferencia. La perpendicular por el extremo C del primer sumando, la corta en el segmento b=AC, que junto con la hipotenusa permite completar la construcción.