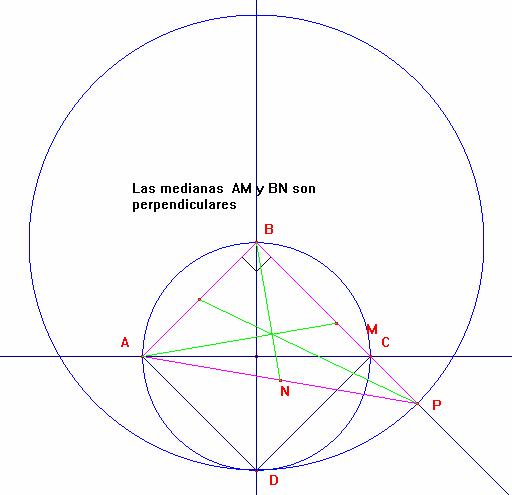
Problema 198     Construir un triángulo rectángulo cuya hipotenusa mide 12 cm, sabiendo que dos de sus medianas son perpendiculares. García Capitán, F (2004): Propuesta personal

Solución Solución de William Rodríguez Chamache. profesor de geometria de la "Academia integral class" Trujillo- Perú (27 de octubre de 2004) : :

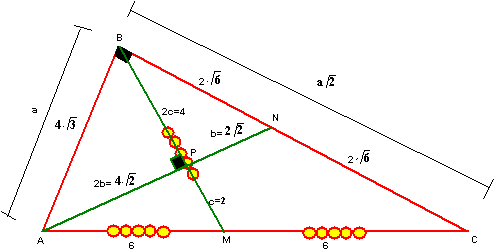
En el triángulo BAN: (2c)²= 2b*b……..  2c²= b²  ….(I)

Luego en el triángulo. APM: 4b²+c²=36  …….(II)

Reemplazando (I) en (II)  obtenemos: c=2 y b=

Construcción:

Con los datos c=2 y b=  determinamos que el triángulo cuyas medianas son perpendiculares es  aquel cuyos catetos son:  y

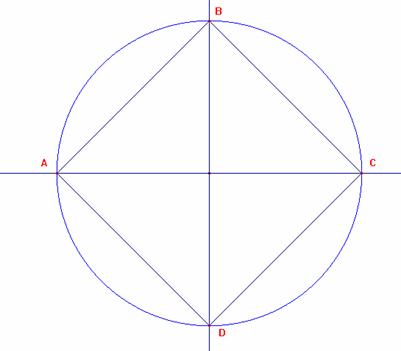
1 Contruimos el cuadrado ABCD para eso  tomamos una circunferencia y trazamos dos diámetros perpendiculares que cortan a la circunferencia en los puntos A, B, C y D que son vértices del cuadrado cuyo lado es AB=a y su diagonal es

2) Tomando como centro el punto B trazamos la circunferencia de radio BD=

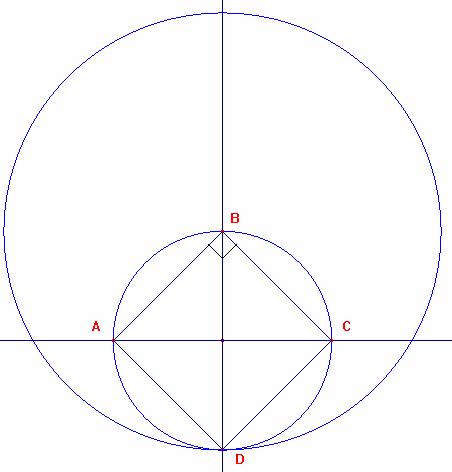
3) Prolongamos el lado BC hasta cortar a la circunferencia en el punto P

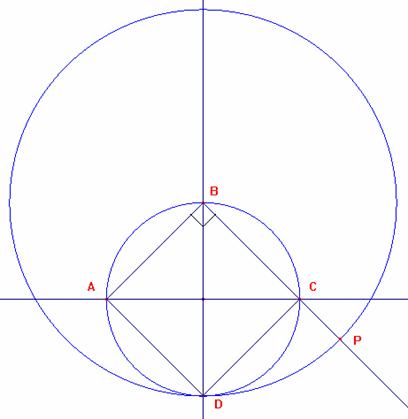
4) finalmente el triángulo buscado será ABP: que tendrá sus medianas perpendiculares

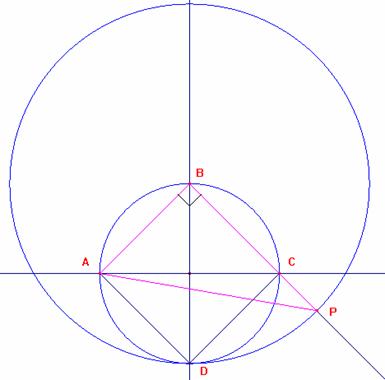
5) finalmente llegamos a la conclusión que todo triángulo rectángulo de catetos que estén en la relación: a y  tendrá dos medianas perpendiculares.