Problema 199
De
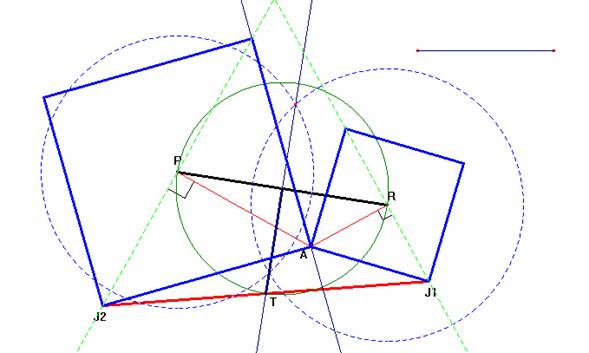
Un día nos encontramos con un libro de matemáticas serio (T. Saati, (1963), Métodos matemáticos de investigación de las operaciones, Ed. Voenizdat, ruso) con un problema que nos pareció que había llegado de las obras de Conan Doyle o Stevenson: En éste se trataba de las búsquedas de un tesoro. Cierta persona se enteró de que en el lugar donde hay enterrado un tesoro crecen solamente tres árboles: un roble, un pino y un abedul. Para encontrar el tesoro hay que situarse debajo del abedul, (A), volviéndose de cara a la línea recta que pasa a través del roble y el pino (R y P). En este caso el roble ha de estar a la derecha y el pino a la izquierda. Luego es necesario dirigirse al roble contando los pasos. Al llegar al roble se vira en ángulo recto hacia la derecha y se da la misma cantidad de pasos que se dio entre el abedul y el roble. En este punto es necesario detenerse y clavar un jalón (J1).
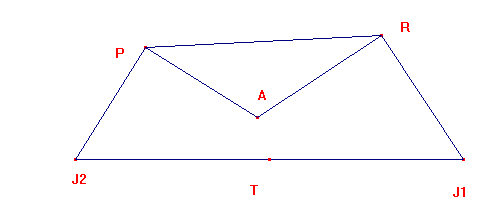
Después hay que regresar al abedul y dirigirse desde este hacia el pino, contando los pasos. Al llegar al pino se vira en ángulo recto hacia la izquierda y se da la misma cantidad de pasos que se dio entre el abedul y el pino. En este punto es preciso detenerse y calvar otro jalón (J2). El tesoro está enterrado precisamente en el centro entre los jalones (en la figura, T). En presencia de una instrucción tan detallada, las búsquedas no pudieron provocar dificultades. Sin embargo, éstas a pesar de todo surgieron. Resultó que cuando el buscador del tesoro llegó al terreno indicado sólo encontró el roble y el pino. No había ni señal del abedul. Pero con todo, encontró el tesoro. Surge la pregunta, ¿cómo logró hacerlo?.
Lyúbich, Y.I., Shor, L.A. (1976, original ruso, 1978 edición en español. ). Método cinemática en problemas geométricos. Lecciones populares de matemáticas. Editorial Mir. Moscú. (traducción de Lozhkin, G.A.). (pág 9,10
SOLUCIÓN AL PROBLEMA 199 (12 de noviembre de 2004)
Profesoras Fabiola Czwienczek Müller y Martha Iglesias Inojosa
Universidad Pedagógica Experimental Libertador
Maracay – Estado Aragua
· Hemos considerado conveniente realizar algunas consideraciones didácticas sobre
1. Realizamos una construcción consistente con regla y compás usando el Cabri II.
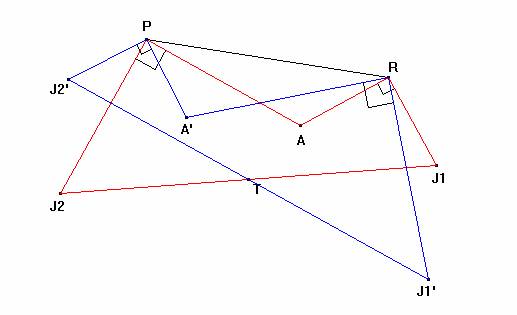
2. “Dinamizando” el punto A, observamos que el punto T es invariante; es decir, los segmentos de la forma J1J2 tienen como punto medio a T. Por lo tanto, la ubicación del tesoro T es independiente de la posición del abedul A.
3. ¿Cómo localizar el punto T en función de los puntos P y R? Parece que T equidista de P y R y, de ser esto cierto, estaría en la mediatriz del segmento PR (en el plano del triángulo PARA). Así que procedimos a trazar la mediatriz del segmento PR y verificar que el punto T pertenece a dicha recta. Es más, el punto T está en la intersección de la mediatriz con la circunferencia de diámetro PR.
4. Es decir, una vez que visualizamos las relaciones existentes entre los “objetos geométricos” que intervienen en dicha construcción, procedimos a formular una conjetura, solamente nos quedaba validarla.
5. Aquí, tuvimos mucha buena suerte, Fabiola recordó la solución del problema 26 publicado en este mismo sitio. Ella envió una de las soluciones publicadas.

6. Por consiguiente, el triángulo PRT es isorrectángulo, con ángulo recto en T. Como PT = TR, T está en la mediatriz del segmento PT. Por ser recto el ángulo PTR, T está en la circunferencia con centro en el punto medio del segmento PR y de radio PR/2.