Problema 199 De la Introducción: Un día nos encontramos con un libro de matemáticas serio (T. Saati, (1963), Métodos matemáticos de investigación de las operaciones, Ed. Voenizdat, ruso) con un problema que nos pareció que había llegado de las obras de Conan Doyle o Stevenson: En éste se trataba de las búsquedas de un tesoro. Cierta persona se enteró de que en el lugar donde hay enterrado un tesoro crecen solamente tres árboles: un roble, un pino y un abedul. Para encontrar el tesoro hay que situarse debajo del abedul, (A), volviéndose de cara a la línea recta que pasa a través del roble y el pino (R y P). En este caso el roble ha de estar a la derecha y el pino a la izquierda. Luego es necesario dirigirse al roble contando los pasos. Al llegar al roble se vira en ángulo recto hacia la derecha y se da la misma cantidad de pasos que se dio entre el abedul y el roble. En este punto es necesario detenerse y clavar un jalón (J1). Después hay que regresar al abedul y dirigirse desde este hacia el pino, contando los pasos. Al llegar al pino se vira en ángulo recto hacia la izquierda y se da la misma cantidad de pasos que se dio entre el abedul y el pino. En este punto es preciso detenerse y calvar otro jalón (J2). El tesoro está enterrado precisamente en el centro entre los jalones (en la figura, T). En presencia de una instrucción tan detallada, las búsquedas no pudieron provocar dificultades. Sin embargo, éstas a pesar de todo surgieron. Resultó que cuando el buscador del tesoro llegó al terreno indicado sólo encontró el roble y el pino. No había ni señal del abedul. Pero con todo, encontró el tesoro. Surge la pregunta, ¿cómo logró hacerlo? Lyúbich, Y.I., Shor, L.A. (1976, original ruso, 1978 edición en español. ). Método cinemática en problemas geométricos. Lecciones populares de matemáticas. Editorial Mir. Moscú. (traducción de Lozhkin, G.A.). (pág 9,10) Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona)
Este problema es muy conocido en el mundo matemático y con una redacción original basada en piratas y tesoros en una isla desierta... Lo cierto es que yo he visto este problema propuesto en multitud de campos de los que puedo enumerar: 1 problema de álgebra 2 problema de cálculo (estudio del cuerpo de los números complejos) 3 problema de geometría analítica 4 problema de álgebra vectorial 5 problema de mecánica 6 problema de geometría analítica 7 problema de geometría afín 8 problema de geometría proyectiva Para mi el procedimiento más elegante y conciso es la solución en el cuerpo de los complejos; y el último que he encontrado es la solución de Jean-Claude Sidler en su Géométrie projective: Cours, exercices et problèmes corrigés. 2e. Édition. Dunod, Paris 2000. Estas dos son las soluciones que expondré

SOLUCION EN EL CUERPO DE LOS COMPLEJOS
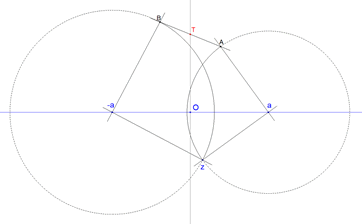Figure 1
a	Tomamos a la recta por el roble y el pino como la recta real Elegimos el punto medio entre el roble y el pino como punto 0 Llamamos a al afijo del roble Llamamos -a al afijo del pino Llamamos z al afijo del abedul
b	Ir del abedul al roble y girar en ángulo recto a la izquierda y recorrer los mismos pasos, en el mundo de los complejos equivale a decir: multiplicamos (z-a) por e^-iπ/2
c	Ir del abedul al pino y girar en ángulo recto a la derecha y girar en ángulo recto y recorrer los mismos pasos, en el mundo de los complejos equivale a decir: multiplicamos (z+a) por e^iπ/2
d	el punto medio es la semisuma

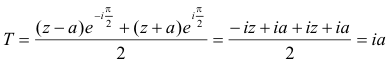
De donde el tesoro está en la mediatriz de roble y pino a la mitad de distancia de los dos robles contando como positiva la dirección del pino al roble. ¡z desaparece y por tanto la solución no depende del abedul!

SOLUCION EN EL PLANO PROYECTIVO Jean-Claude Sidler exercice 4.18
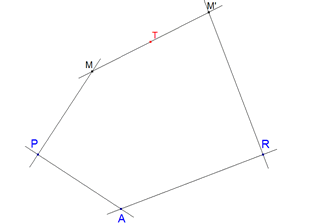Figure 2
Se puede encontrar el tesoro partiendo de un punto cualquiera A diferente de P y de R; en efecto, se pasa de M a M’ componiendo la rotación de centro P y ángulo π/2 seguido de una rotación de centro R y ángulo π/2, es decir, por una simetría central cuyo centro es el punto medio de MM’