Problema 199
Solución de William Rodríguez Chamache, profesor de geometría de la "Academia integral class" Trujillo- Perú,
Sean P y R las ubicaciones de los Árboles Pino y Roble

Trazamos la recta que contiene a los puntos P y R

Bajo los puntos P y R asumimos una posición cualquiera del punto A (abedul) puesto que no sabemos donde estará ubicado
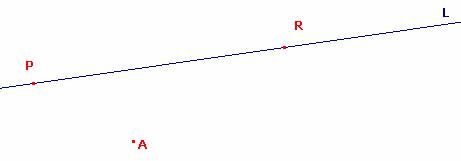
Luego unimos los punto A y P; A y R determinándose los segmentos AP y AR
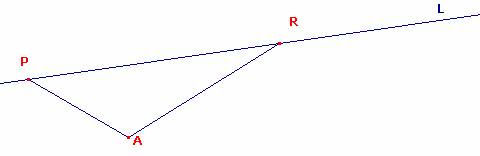
Según el problema levantamos perpendiculares por los puntos P y R a los segmentos PA y RA ubicados en el semiplano que contiene al punto A (abedul) de manera que PA=PJ2 y RA=RJ1

ahora sabemos que el tesoro se encuentra en el punto medio del segmento J2J1 entonces trazamos la recta que pasa por los puntos J1 y J2
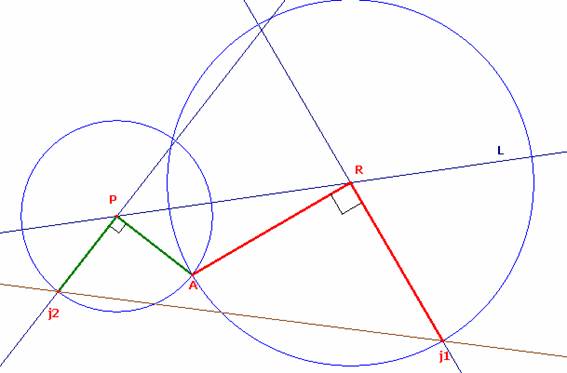
Luego trazamos las perpendiculares J2M, AT y J1N al recta L determinándose los triángulos iguales PMJ2=PAT y TAR=RNJ1 (LAL)
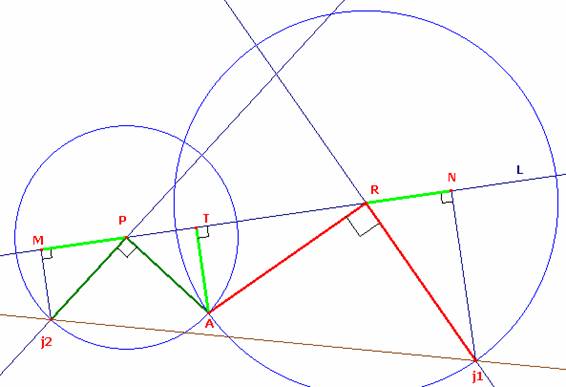
Luego sea determinado un trapecio rectángulo J2MNJ1 estando el tesoro ubicado en el punto medio del segmento J2J1 para eso por el punto medio del segmento que conocemos PR levantamos su mediatriz que cortara al segmento J2J1 en su punto medio T (tesoro)
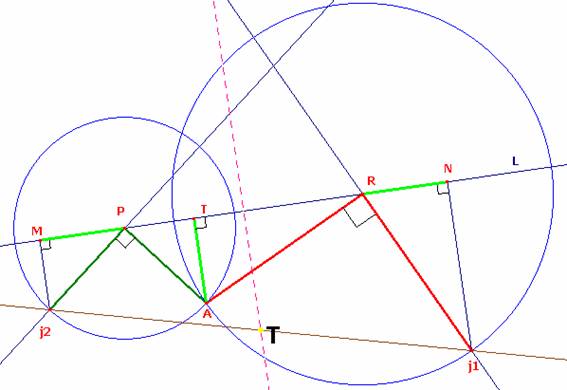
En el applet observaremos que el punto A se puede tomar en un punto cualquiera solo se debe tener en cuenta los segmentos iguales y perpendiculares PA=PJ2 y AR=RJ1
Indudablemente la persona que encontró el tesoro tenía un amplio conocimiento sobre geometría
Prof.: William Rodríguez Chamache