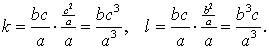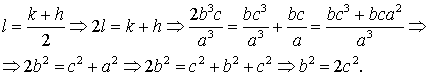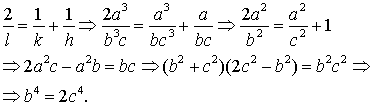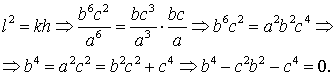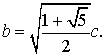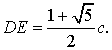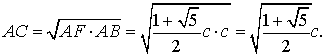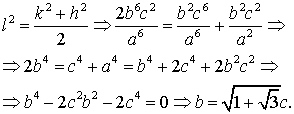Problema 200 de triánguloscabri

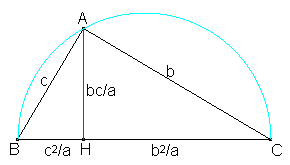
Sea H el pie de la perpendicular trazada desde el vértice A sobre el lado BC del triángulo ABC que es rectángulo en A.

Por H trazamos las perpendiculares sobre los lados AB y AC, obteniendo los pies sobre estos lados que denotamos por F y G, respectivamente.

Por último, desde F y G dibujamos las perpendiculares sobre el lado BC, obteniendo los puntos K y L respectivamente.

Supongamos que el cateto b=AC sea mayor que el c=AB. Llamemos k=FK, l = GL y h=AH.

Caracterizar y construir todos los triángulos rectángulos tales que

l sea media armónica de k y h,
l sea media geométrica de k y h,
l sea media aritmética de k y h,
l sea media cuadrática de k y h.

Solución de Francisco Javier García Capitán, IES Alvarez Cubero de Priego de Cçordoba

Comencemos por observar el hecho conocidísimo de que los triángulos ABC, HBA y HAC son semejantes, de donde es fácil deducir las medidas de los segmentos AH, BH y CH, mostradas en la figura. A la vez, el hecho de que AH²=BH·HB, da una construcción sencilla de la raíz cuadrada del producto de dos segmentos: Ponemos los dos segmentos sobre una recta, uno a continuación del otro, trazamos la circunferencia que tiene por diámetro al resultado de ello y levantamos por el punto de unión de los dos segmentos una perpendicular a la recta. Esta perpendicular corta a la circunferencia en un punto que determina un segmento cuya medida es la mencionada raíz cuadrada.

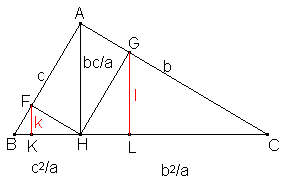
Al hacer la construcción especificada por el enunciado, los triángulos ABC, FBH y GHC son semejantes, de donde podemos deducir las medidas de las k y l.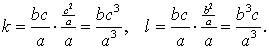

En el caso de la media aritmética tenemos:

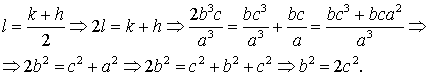
Por tanto, uno de los catetos es al otro como la diagonal de un cuadrado al lado. Fijado el segmento AB = c, levantamos el cuadrado ABDE sobre él. Entonces será 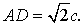Con centro A y radio AD trazamos un arco que corta a AE en C, cumpliéndose evidentemente que

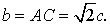
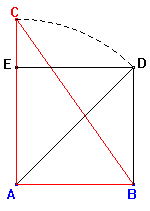
Usaremos la construcción anterior como auxiliar para la construcción en el caso de la media armónica, en la que tenemos:

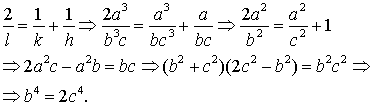
Partimos de AB = c y construimos como antes C de manera que 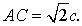Ahora construimos B' por el otro lado de manera que AB' es perpendicular a AB y AB' = c. Después, trazamos la circunferencia con diámetro CB' y hallamos la intersección C' de dicha circunferencia con la perpendicular a CB' por A. Tendremos que

Pasamos ahora al interesante caso de la media geométrica. Ahora los cálculos son:

Resolviendo la ecuación bicuadrada en b, y teniendo en cuenta que b es mayor que c, obtenemos que

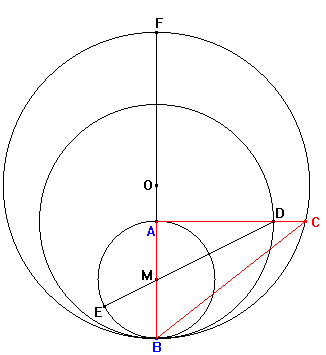
(Observemos de paso que el número que hay bajo la raiz grande es el número de oro.) Partimos de AB=c y hacemos AD=c perpendicular a AB. Siendo M el punto medio de AB y E el punto de corte de la recta DM con la circunferencia de diámetro AB, tal como se muestra en la figura, tendremos

Para obtener la raíz cuadrada de este número prolongamos BA hasta F de manera que AF=DE y trazamos la circunferencia con diámetro BF. La perpendicular a BF por A cortará a esta circunferencia en el vértice C del triángulo buscado, pues

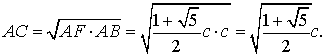
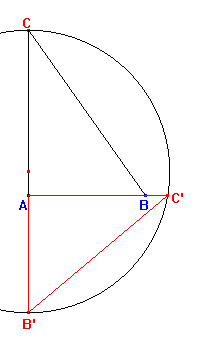
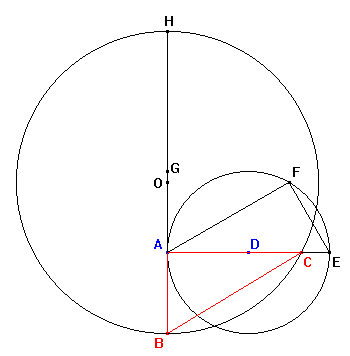
Para terminar, resolvamos el caso de la media cuadrática.

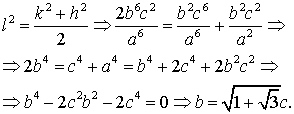
De nuevo aparecen las raíces cuadradas.

De nuevo, partimos del segmento AB = c. Para construir un segmento igual a 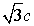construimos perpendicular a AB un segmento AE = 2 AB y hallamos un punto F sobre la circunferencia con diámetro AE tal que EF = AB. Aplicando el teorema de Pitágoras al triángulo AEF tendremos que AF = .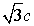

Ahora prolongamos BA hasta G de manera que AG=BA y BG hasta H de manera que GH = AF. Entonces tendremos que AH = 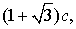y ya solo queda hallar la raíz cuadrada. para lo cual trazamos la circunferencia con diámetro BH y el punto de intersección C con la perpendicular a AB trazada por A.