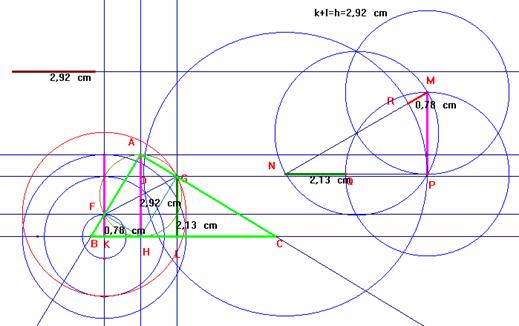
Problema 200.-
Solución de William Rodríguez Chamache. profesor de geometria de la "Academia integral class" Trujillo- Perú (10 de noviembre de 2004)
Caracterizar y construir todos los triángulos rectángulos tales que
1.- l sea media armónica de k y h,
Solución:
Sabemos que debe de cumplirse: 
Del grafico observamos que: 
resolviendo estas dos ecuaciones
……………………. 
Luego reemplazando en: obtenemos:
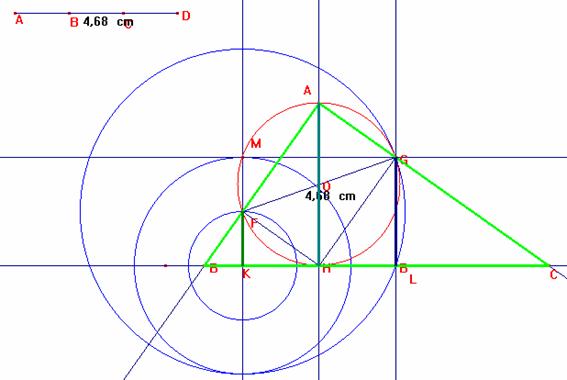
Construcción:
1) Construimos el triángulo rectángulo isósceles de 45º de cateto k entonces la hipotenusa será 
2) Ahora sobre una recta levantamos los segmentos perpendiculares KF=k, y
KT=
3) Ahora sabemos que la distancia que separa los vértices F y G es 
luego del punto medio O de FG se traza la perpendicular OH^BL y prolongando HO hasta el punto A de manera que HO=OA entonces el rectángulo FAGH tiene como diagonales los segmentos AH=FG=, finalmente al prolongar AF y AG se determina los puntos B y C por lo tanto el triángulo rectángulo ABC es el triángulo buscado.
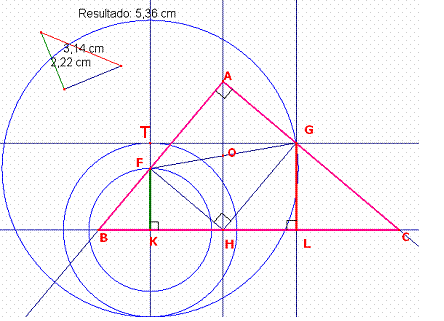
2.- l sea media geométrica de k y h,
Solución:
Sabemos que debe de cumplirse: 
Del gráfico observamos que: 
resolviendo estas dos ecuaciones
……. 
Resolviendo obtenemos: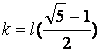 
………. (1)
Luego reemplazando en obtenemos:
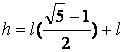
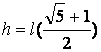………………………………………. (2)
Construcción:
Dato: ……..(a) además se sabe que: ………(b)
Resolviendo estas dos ecuaciones obtenemos:
……… 
Resolviendo: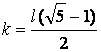 
Ahora reemplazando en (c) en (b):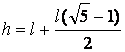 
………
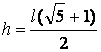
Construcción:
Tomamos un segmento AB=L. Luego por B levantamos la perpendicular BC=L/2 determinado el triángulo Rectángulo ABC de hipotenusa AC= 
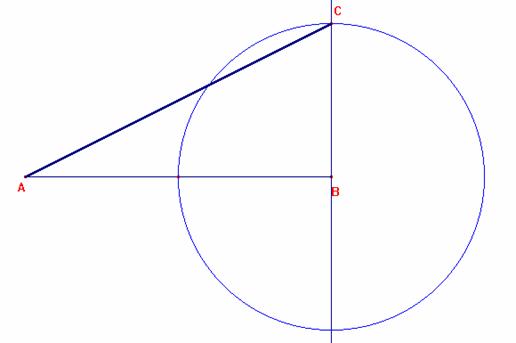
Tomando como centro en C y radio CB se traza la circunferencia que corta a la hipotenusa en el punto D.
Entonces obtenemos que: 
y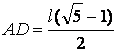 
siendo este valor, k=FH
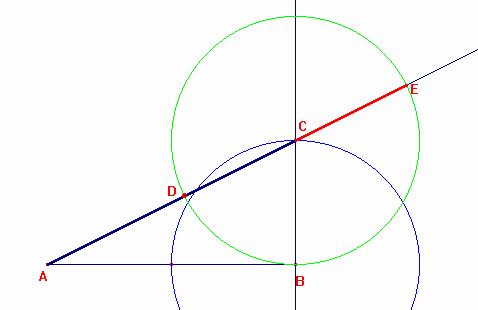
Ahora para obtener el valor de: “h” se prolonga el segmento AD hasta cortar a la circunferencia en el punto E determinadote que: CE=
y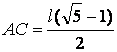 
por lo tanto la medida del segmento 
.
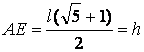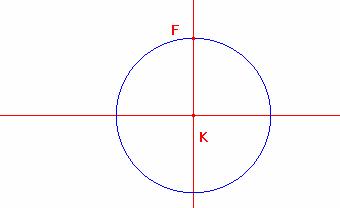
Luego sobre una recta L se toma el punto K y se levanta la perpendicular KF=k
Luego tomando como centro el punto F se traza la circunferencia de radio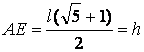
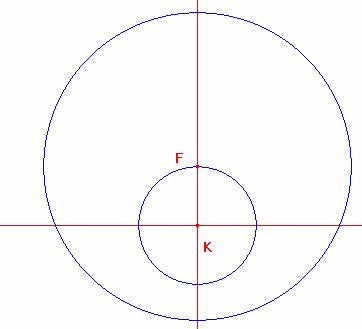
Ahora tomando como centro K y radio AB =L estraza la circunferencia determinándose el segmento FN=AB=L
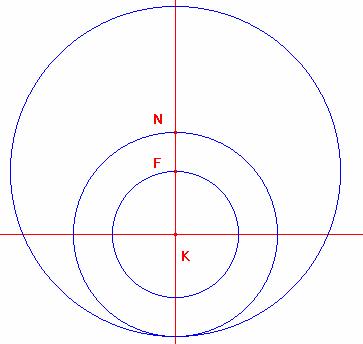
Luego trazamos la perpendicular por N al segmento FK cortando a la circunferencia en el punto G
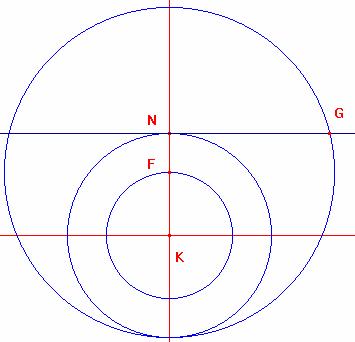
Ahora trazamos la perpendicular GL a la recta que pasa por el punto K,
Ahora tomando el punto medio del segmento FG se determina el rectángulo (igual que en el caso anterior) FAGH.
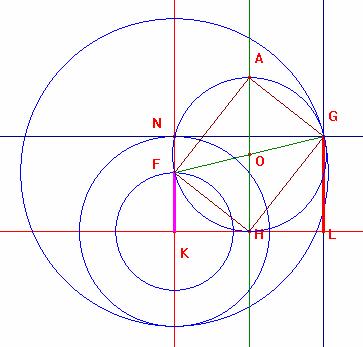
Finalmente prolongando los segmentos AF y AG se determinan los puntos B y C que con el punto A determina el triángulo ABC buscado
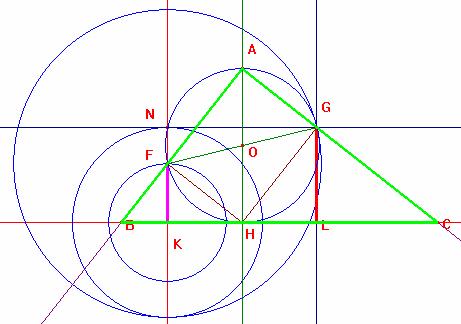
3.- l sea media aritmética de k y h,
Dato: 
además es sabe que: 
De estas ecuaciones obtenemos:
:
Luego 
Construcción:
La construcción es similar a la anterior.
4.- l sea media cuadrática de k y h,
Solución:
Dato: 
; sabemos que: H=k+l
.h=k+l
(h-k)2=l2
h2-2hk+k2=l2
h2-2hk+k2=
h2-4hk+2k2=0
Resolviendo:
h2-4hk+2k2=0
A=1, B=-4h, C=h2
Reemplazando obtenemos: 
; 
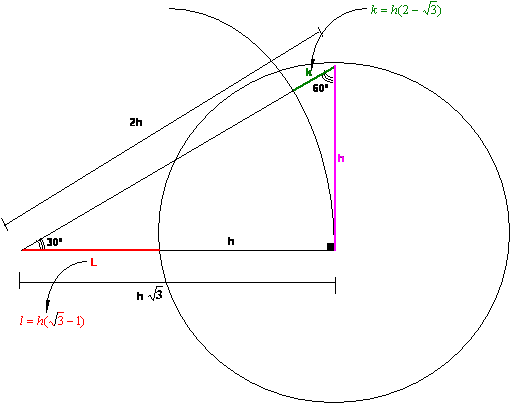
Construcción:
