 Partiendo
del triángulo de referencia ABC, los vértices tienen coordenadas
A=(1:0:0), B=(0:1:0) y C=(0:0:1).
Partiendo
del triángulo de referencia ABC, los vértices tienen coordenadas
A=(1:0:0), B=(0:1:0) y C=(0:0:1).
Problema 202 de triánguloscabri |
|
(o una invitación a las coordenadas
baricéntricas)
|
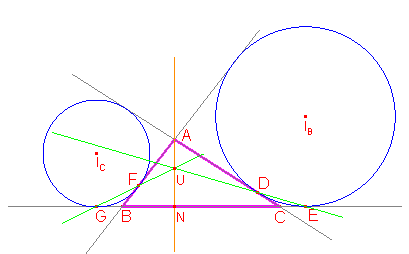
| Sea el triángulo ABC, cuyos excírculos (Ib),(Ic) tienen como puntos de tangencia a (D,E) y (F,G) con (AC, BC) y (AB,BC) respectivamente. Demostrar que FG y DE se cortan en la altura ha del triángulo ABC. |
|
Propuesto por Juan Carlos Salazar
|
Solución de Francisco Javier García Capitán (con coordenadas baricéntricas).
Usaremos las coordenadas baricéntricas para resolver este problema y, recíprocamente, usaremos este problema para introducir las coordenadas baricéntricas.
Un punto de partida para aprender sobre coordenadas baricéntricas puede ser mi trabajo (incompleto) Coordenadas baricéntricas, y para profundizar bastante más está lo que yo creo la obra de referencia, Introduction to the Geometry of the Triangle, de Paul Yiu.
Considerando un triángulo de referencia ABC, un punto P tendrá coordenadas baricéntricas (u:v:w) cuando los triángulos PBC, PCA y PAB tengan áreas (con signo) proporcionales a u:v:w (las coordenadas baricéntricas son únicas salvo un factor de proporcionalidad).
 Partiendo
del triángulo de referencia ABC, los vértices tienen coordenadas
A=(1:0:0), B=(0:1:0) y C=(0:0:1).
Partiendo
del triángulo de referencia ABC, los vértices tienen coordenadas
A=(1:0:0), B=(0:1:0) y C=(0:0:1).
Cualquier punto que esté en la recta BC tendrá coordendas de la forma (0:v:w). En ese caso tendremos que BP:PC = w:v (teniendo en cuenta de nuevo las medidas con signo). Por ejemplo, teniendo en cuenta que GB = s—a, siendo s el semiperímetro de ABC y, como es habtual a=BC, tendremos que BG : GC = —(s—a):s, por lo que podemos expresar G = (0: —s, s—a). Análogamente será E=(0: s—a : —s).
Análogamente, en la recta AB el punto F cumple que AF:FB = s—b:s—a, por lo que F=(s—a:s—b:0), y análogamente, D=(s—a:0:s—c).
Hallemos ahora las coordenadas del punto N, pie de la altura trazada por A. Como
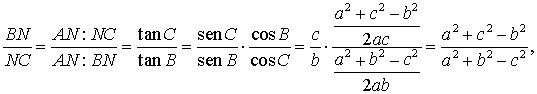
resulta que ![]()
Ahora que ya tenemos calculadas las coordenadas de todos los puntos que intervienen como datos podemos pasar a calcular rectas que pasan por dos puntos y puntos de intersección de rectas. Aquí el uso de coordenadas baricéntricas hace las cosas muy sencillas, porque podemos usar la misma cuenta para efectuar las dos operaciones.
Lo que necesitamos saber para continuar es que:
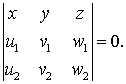
![]()
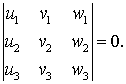
El lector advertirá que en los dos primeros apartados los coeficientes de la ecuación de la recta y las coordenadas del punto se obtienen exactamente de la misma manera, por lo que pueden calcularse con una misma función de Mathematica:
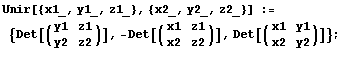
Cada terna representa a un punto o a una recta. La función Unir
aplicada a dos rectas devuelve las coordenadas del punto de intersección,
y aplicada a dos puntos devuelve los coeficientes de la recta que los une.
Una vez introducidos estos conceptos y herramientas, la resolución del problema se reduce a la siguientes instrucciones:
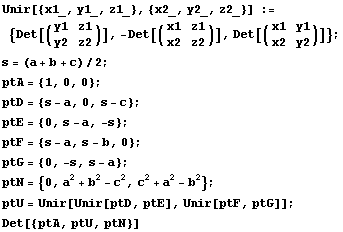
![]()
Como el área del triángulo AUN, calculada con un determinante, es 0, deducimos que U está en la altura AN.
Por no acabar aquí, podemos preguntarnos si el punto U siempre estará en una posición determinada de la recta AN, por lo que vamos a calcular la proporción AU:UN. En este caso, usamos la fórmula de la distancia en coordenadas baricéntricas homogéneas, que es, sencillamente, descomunal:
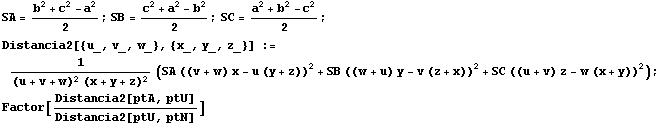
![]()
Descubrimos entonces que siempre es![]()