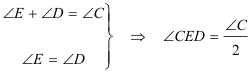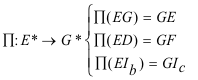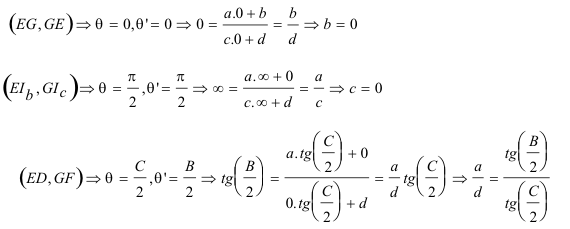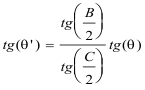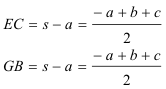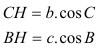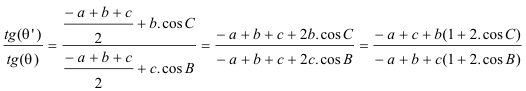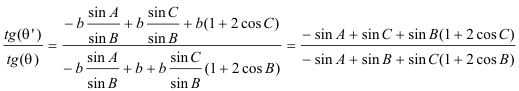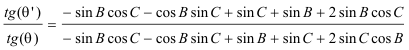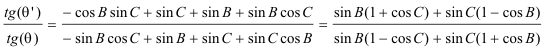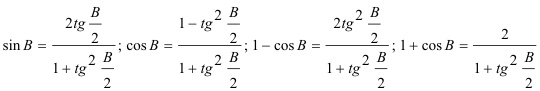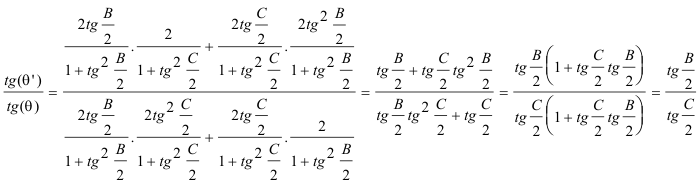Problema 202. Propuesto por Juan Carlos Salazar.

Sea el triángulo ABC, cuyos excírculos (I_b),(I_c) tienen como puntos de tangencia a (D,E) y (F,G) con (AC,BC) y (AB,BC) respectivamente. Demostrar que FG y DE se cortan en la altura h_a del triángulo ABC.

Salazar, J. C. (2004): Propuesta personal

José María Pedret. Ingeniero Naval. Esplugues de Llobregat (Barcelona).

0.1 PROYECCION ENTRE HACES DE RECTAS

TEOREMA 0.1

Cuando dos haces de cuatro rectas que se corresponden una a una, respectivamente, tienen sus razones dobles iguales (son homográficas), si una de las rectas coincide con su imagen, las tres rectas restantes del haz cortan a sus rectas correspondientes en el otro haz en tres puntos situados en línea recta.

(El teorema recíproco no es más que la definición de una proyección entre haces de rectas.)

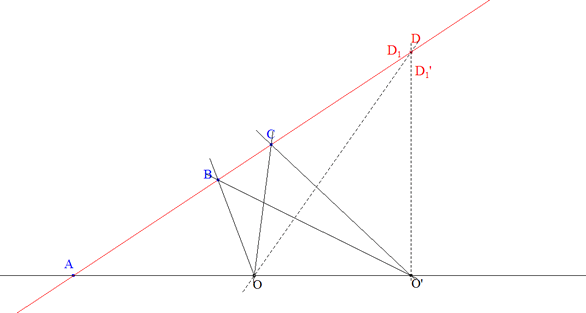
202.2.gif

figura 1

Demostración 2.1

Sean O* y O’* los dos haces. Sean OA, OB, OC, OD (figura 2)las cuatro rectas de O* y O’A, O’B, O’C, O’D las cuatro rectas de O’* que les corresponden respectivamente. Supongamos que las rectas que coinciden son OA y O’A; entonces mostraremos que los puntos de intersección de cada recta con su correspondiente, B=OB∩O’B, C=OC∩O’C, D=OD∩O’D, están en línea recta.

Sean A=BC∩OO’, D₁=BC∩OD y D₁'=BC∩OD’. Como los dos haces son homográficos, conservan la razón doble; tenemos (OA, OB, OC, OD₁)=(O’A, O’B, O’C, OD₁')y por lo tanto D₁=D₁' con lo que OD y O’D se cortan en BC.

0.2 EXPRESION ALGEBRAICA DE UNA HOMOGRAFIA ENTRE HACES DE RECTAS

Al igualar loas razones dobles entre cuatro rectas de un haz y las cuatro rectas correspondientes en el otro haz deducimos la expresión algebraica de una homografía entre haces de rectas.

Sean dos haces de rectas R* y R’*, si m es la tangente de la recta r perteneciente a R* y m’ es la tangente de la recta m’ perteneciente a R’*, la relación homográfica entre ellas se expresa como:

1.0 DETERMINACION DEL ANGULO ∠CED

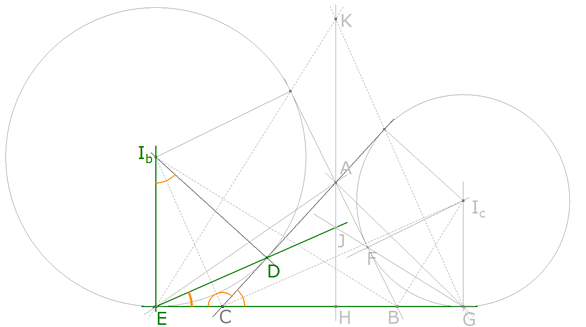
202.1.gif

figura 2

Trazamos el enunciado y observando a fondo la figura deducimos que en la recta EG:

pero como E y D son los puntos de tangencia, en el triángulo ECD se cumple

obtenemos entonces

EL PROBLEMA

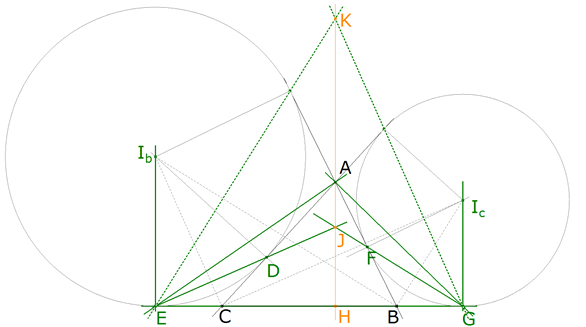
202.3.gif

figura 3

Comprobar que EJ y GJ se encuentran en HA es fácil si E* y G* son dos haces de rectas en proyección. En ese caso, si una de las rectas es imagen de sí misma (TEOREMA 0.1), los puntos de intersección, de las rectas del primer haz con sus homólogas d el segundo, se encuentran sobre una recta. Si esa recta es HA habremos probado el enunciado.

Sean los haces de rectas

Definimos la siguiente homografía entre haces de rectas, Π:E*—>G* y Π(EG)=GE, lo que hace que Π sea una proyección y asegura que cada recta y su imagen se encuentran en una recta

Si θ es el ángulo de cualquier recta de E* con EG y θ’ es el ángulo de cualquier recta de G* con GE, la expresión de esta homografía es

y nos queda

que es la relación homogéfica entre las rectas de los dos haces a través de sus pendientes.

Vamos a determinar ahora el je de proyección de la homografía:

entonces esa recta es paralela a EI_b y a GIc; por lo tanto es perpendicular a EG.

podemos decir que la recta de intersección buscada es la perpendicular a EG que pasa por el punto J.

Pero en el punto A del triángulo

¿ES Π(EA)=GA?

como conocemos (Problema 169) los segmentos que generan los círculos inscritos, escribimos:

y además (ver figura 3)

nos queda

con el teorema del seno

añadiendo que A+B+C=π

y con "un poco" del ángulo mitad

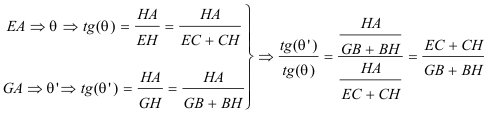
podemos pues decir que

por tanto A está sobre la perpendicular por J a EG; pero la perpendicular por A a EG es la altura del triángulo y por tanto J está sobre la altura

que es lo que queríamos demostrar*.

*Por el mismo método podríamos ver (figura 3) que la recta que une G con el otro punto de contacto distinto de F y la recta que une E con el otro punto de contacto distinto de D se cortan en K que también se encuentra sobre la altura.