Problema 203 .

Siga el triangle  tal que .

Siga H el peu de l’altura traçada des de B sobre el costat .

Siguen K, J els punts migs del costat  i del segment  respectivament.

Siga L el punt que s’obté com intersecció de la recta que passant per J és paral·lela al costat  talla el costat .

Proveu que:

a)      El triangle  és equilàter.

b)     

c)     

d)  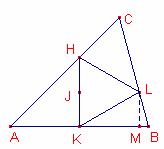       Nota: .

Solució de Solución deRicard Peiró i Estruch Profesor de Matemáti cas del IES 1 de Xest (València) (17 de noviembre de 2004) (en valenciano):

a)

Siga  tal que .

Siga . Aleshores, .

Siga H el peu de l’altura traçada des de B sobre el costat .

 és rectangle.

.

El triangle  és isòsceles, aleshores  és la seua altura.

El triangle  és rectangle isòsceles. Aleshores, .

Siga M el peu de la perpendicular traçada des del punt L sobre el costat .

Considerem el triangle rectangle . Aplicant raons trigonomètriques:

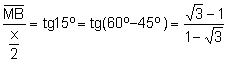
Aleshores, .

Siga  

El triangle  és rectangle. Aplicant raons trigonomètriques:

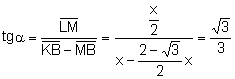. Aleshores, .

.

El triangle  és isòsceles ja que  és mediatriu de .

Per tant, El triangle  és equilàter.

b)

Calculem les àrees dels triangles , .

L’àrea del triangle equilàter  de costat x és:

.

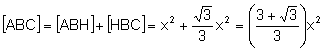
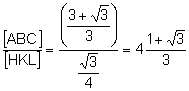c)

Els triangles ,  tenen la mateixa base . Aleshores la proporció de les àrees és igual a la proporció de les altures:

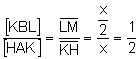
d)

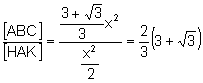     (1)

Aplicant c):

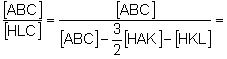
Aplicant b) i (1):

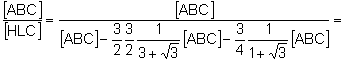
Simplificant:

.