Problema 203 .

Sea el triángulo  tal que .

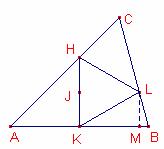
Sea H el pie de la altura trazada desde B sobre el lado .

Sean K, J los puntos medios del lado  y del segmento  respectivamente.

Sea L el punto que se obtiene como intersección de la recta que pasando por J es paralela al lado  corta el lado .

Probar que:

a)      El triángulo  es equilátero.

b)     

c)     

d)         Nota: .

Solución deRicard Peiró i Estruch Profesor de Matemáticas del IES 1 de Xest (València)(17 de noviembre de 2004) (en español)

:

a)

Sea  tal que .

Sea . Entonces, .

Sea H el pie de la altura trazada desde B sobre el lado .

 es rectángulo.

.

El triángulo  es isósceles, entonces  es la altura.

El triángulo  es rectángulo isósceles. Entonces, .

Sea M el pie de la perpendicular trazada des del punto L sobre el lado .

Consideramos el triángulo rectángulo . Aplicando razones trigonométricas:

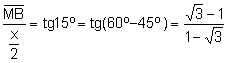
Entonces, .

Sea  

El triángulo  es rectángulo. Aplicando razones trigonométricas:

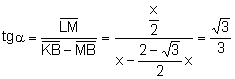. Entonces, .

.

El triángulo  es isósceles ya que  es mediatriz de .

Por tanto, El triángulo  es equilátero.

b)

Calculemos las áreas de los triángulos , .

El área del triángulo equilátero  de lado x es:

.

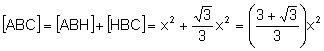
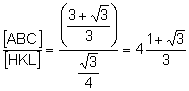c)

Los triángulos ,  tienen la misma base . Entonces la proporción de las áreas es igual a la proporción de las alturas:

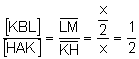
d)

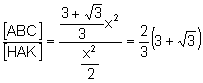     (1)

Aplicando c):

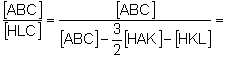
Aplicando b) y (1):

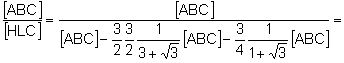
Simplificando:

.