Problema 203
Propuesto por Juan Bosco Romero Márquez
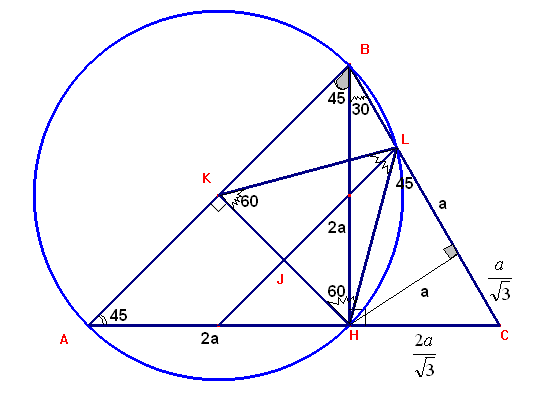
Sea ABC un triángulo en el que < C=60, < B=75, <A = 45.
Sea H el pie de la altura trazada desde B sobre el lado AC.
Los puntos K y J son los puntos medios del lado AB y del segmento HK respectivamente.
El punto L se obtiene como intersección de la recta que pasando por J es paralela al lado AB al cortar al lado BC.
Probar que:
• El triángulo HKL es equilátero inscrito en el ABC.
• [ABC]/ [HKL] = 4 ((sqr(3))+1)/3
• [KBL] = [HAK]/2
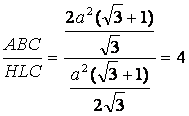
• [ABC] / [HLC] = 4
Romero, J.B. (2004): Comunicación personal.
Solución de William Rodríguez Chamache. profesor de geometria de la "Academia integral class" Trujillo- Perú (19 de noviembre de 2004) :
Primero algunas consideraciones
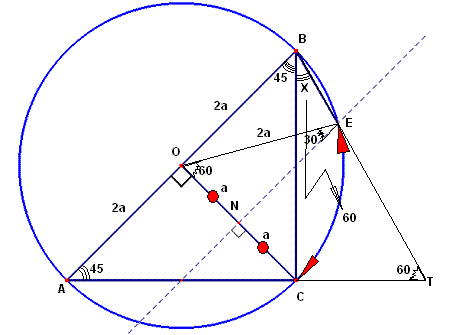
1) En la figura mostrada hallar “x” si EN //AB y N punto medio de OC.
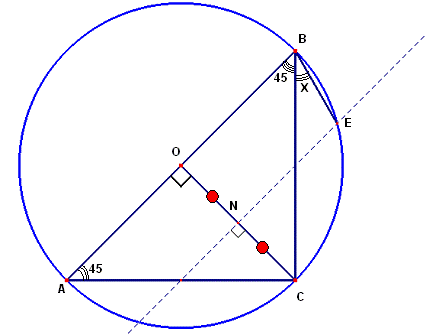
Sea: AO=OB=2 a; entonces. ON=NC=a, luego observamos que el triángulo ONE es notable de 30 y 60 por lo tanto el arco EC=60 y el ángulo x=30 (por ser ángulo inscrito)
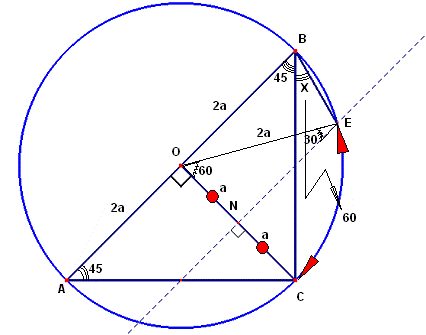
Ahora si prolongamos los segmentos BE y AC se intersecan en el punto T generando la figura indicada en el problema 203.
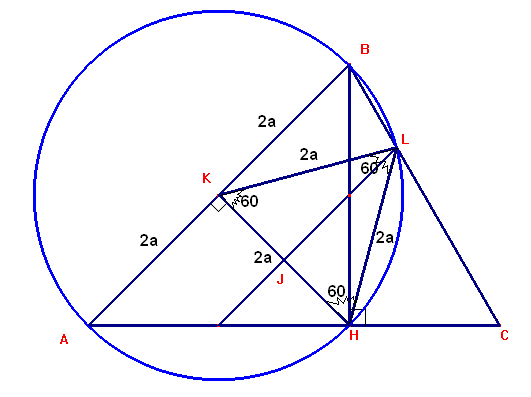
Probar que:
• El triángulo HKL es equilátero inscrito en el ABC.
Ahora según la figura del problema determinamos que el punto L pertenece a la circunferencia circunscrita al triángulo ABH. Por lo tanto el cuadrilátero ABLH es inscriptible y el triángulo KHL es equilátero
Probar que:
• [ABC]/ [HKL] = 4 ((sqr(3))+1)/3
Del gráfico anterior determinaremos las medidas de los segmentos.: BH, AH y HC
Del gráfico observamos que: ![]() ,
, ![]() y
y 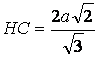
Calculando el área del triángulo 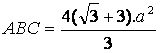 y el área del triángulo
y el área del triángulo 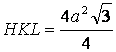 finalmente se obtiene:
finalmente se obtiene: 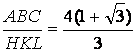
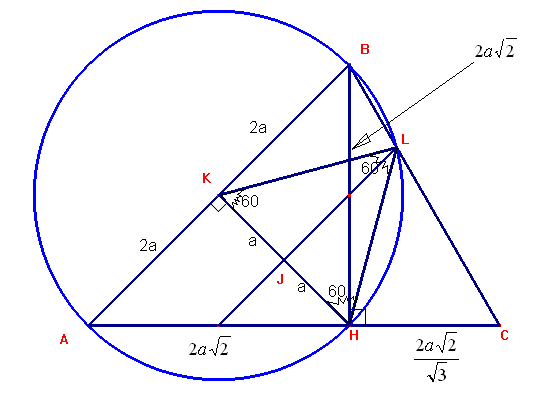
Probar que: [KBL] = [HAK]/2
El area Del triángulo ![]()
El area deol triángulo ![]()
Finalmente: ![]()
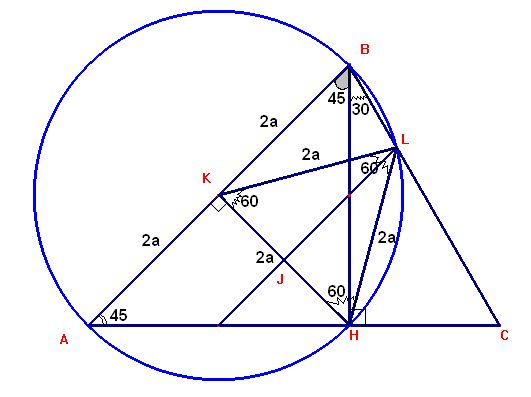
Probar que:
• [ABC] / [HLC] = 4
Del gráfico se cumple que: