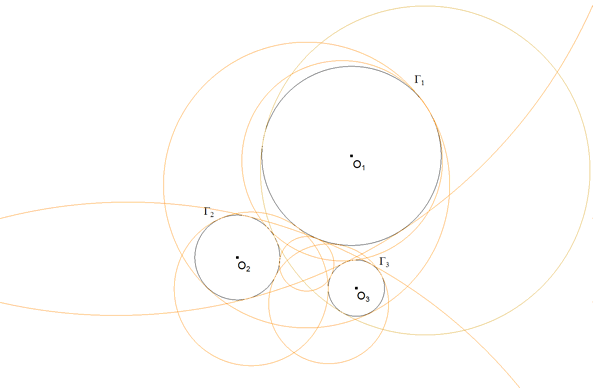
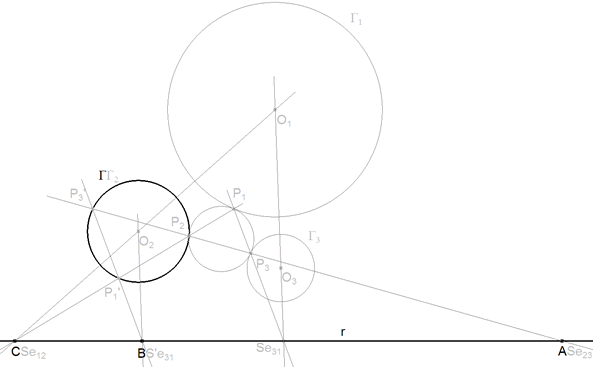Problema 204

EL PROBLEMA DE APOLONIO Y EL PROBLEMA DE CASTILLON

José María Pedret. Ingeniero Naval. Esplugues de Llobregat (Barcelona).

TRAZAR EL CÍRCULO TANGENTE A TRES CÍRCULOS DADOS.

No parece, éste, el problema más adecuado para una revista especializada en triángulos; pero si transformamos el problema de buscar el círculo tangente por el problema de buscar el triángulo que pasa por los puntos de contacto ya habremos dado un paso hacia el mundo de los triángulos. Se objetará que los puntos de contacto no se conocen; pero si estudiamos la figura propuesta, podemos, de nuevo, encontrar un triángulo vinculado al anterior cuyos lados pasan por tres puntos conocidos y está inscrito en uno de los círculos dados.

JULIUS PETERSEN en Métodos y teorías para la resolución de problemas de construcciones geométricas propone el problema de Apolonio como problema 403 y aunque no es el método que desarrolla, indica lo siguiente:

403. TRAZAR UN CIRCULO TANGENTE A TRES CIRCULOS DADOS

...Se puede también resolver por un procedimiento que es completamente igual al que se aplica al problema 201*. El triángulo que se trata de construir es aquel cuyos vértices coinciden con los puntos de contacto buscados; sus lados pasan por tres de los centros de semejanza de los círculos dados. Si tomamos esos puntos como centros de inversión eligiendo las potencias de inversión de tal manera que dos cualesquiera de los círculos se intercambian entre ellos, cada uno de los círculos después de tres inversiones volverá a la posición inicial. No hay pues diferencia esencial entre el problema que nos ocupa y el que ya ha sido resuelto anteriormente...

*El problema 201 en el libro de Petersen corresponde al problema de Castillon

Resolvamos el problema de Apolonio:

TRAZAR UN CIRCULO TANGENTE A TRES CIRCULOS DADOS

Primero Pasar del problema de Apolonio al problema de Castillon

Segundo Aplicación a resolver el problema original de Apolonio

Pedret, J.M. (2004): Comunicación personal

Solución de José María Pedret, Ingeniero naval. Esplugues de Llobregat (Barcelona). (16 de novimbre de 2004)

0. INTRODUCCION

Para atender la sugerencia de Julius Petersen, debemos ser maestros en el uso de la inversión. Nosotros como Apolonio intentamos resolver el problema usando las herramientas más simples que nos proporciona la GEOMETRIA “ANTIGUA”.

En el APARTADO UNO, reflejamos un mínimo de proposiciones elementales que son tan conocidas que hacemos uso de ellas sin establecer la demostración.

En el APARTADO DOS demostramos siete proposiciones básica para el planteamiento y resolución del problema que nos ocupa:

— Establecemos la existencia de un punto notable vinculado a los tres círculos dados. Este punto es el centro radical, nombre que no existía en la antigüedad. Lo definimos y lo construimos sin acudir a tangentes ni potencias ni ejes radicales.

— Luego establecemos la existencia de otros seis puntos notables vinculados a los tres círculos dados (tomados dos a dos). Estos puntos se denominan centros de semejanza, nombre que tampoco existía en la antigüedad.

— Ponemos de manifiesto cuatro rectas sobre las que se encuentran los centros de semejanza. Estas rectas son los denominados, hoy en día, ejes de semejanza.

— Acabamos el apartado poniendo de manifiesto la alineación de puntos de contacto y establecemos una propiedad interesante sobre el paralelismo de dos cuerdas en dos círculos tangentes.

A partir de aquí, para desarrollar el APARTADO TRES,

— suponemos el problema resuelto y estudiamos la figura y vemos la disposición de los puntos de contacto en la solución.

— Aplicamos el mencionado teorema de las cuerdas paralelas y descubrimos la existencia de tres puntos sobre uno de los círculos dados que son los vértices de un triángulo auxiliar que pasa por dos de los centros de semejanza y un tercer punto sobre el eje que definen.

— En 3.4 enunciamos el Problema de Castillon equivalente, una vez determinado ese tercer punto.

En el APARTADO CUATRO, podíamos usar nuestro conocimiento del Problema de Castillon y llegar hasta el final; pero Pappus solucionó de forma fácil el caso en que los tres puntos están sobre una recta y éste es el que resolvemos.

— Determinado el triángulo auxiliar, determinamos los puntos de contacto del problema original y trazamos el círculo tangente pedido.

— Para cada eje de semejanza, y de acuerdo con el Problema de Castillon, la solución es doble . Como hay cuatro ejes, habrá como máximo, ocho soluciones.

Y por fin en el APARTADO CINCO resolvemos EL PROBLEMA DE APOLONIO PROPIAMENTE DICHO.

— Aplicamos a cada eje lo desarrollado en los apartados anteriores y obtenemos la solución que proporciona en general ocho círculos tangentes a los tres dados.

1. TEOREMAS PREVIOS SIN DEMOSTRACION

Incluimos en este apartado, sólo para hacer memoria, una serie de construcciones y teoremas de los que, por conocidos, obviamos la demostración.

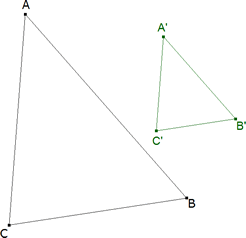
figura1

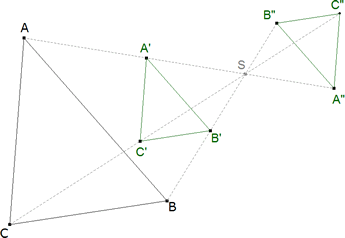
Dos triángulos ABC y A’B’C’ son semejantes si tienen:

TEOREMA 1.1 dos ángulos correspondientes iguales,

TEOREMA 1.2 un ángulo igual comprendido entre lados proporcionales,

TEOREMA 1.3 los lados proporcionales,

figura 2

TEOREMA 1.4 Si en dos triángulos ABC y A’B’C’ de lados paralelos unimos dos a dos los vértices correspondientes A y A’, B y B’, C y C’ `por medio de rectas, estas tres rectas se cortan en un punto.

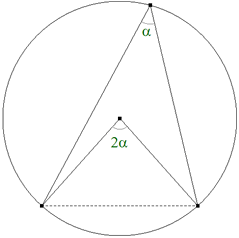
figura 3

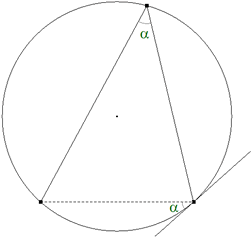
TEOREMA 1.5 El ángulo en el centro es el doble que el ángulo en la circunferencia. Si la cuerda es el diámetro, α = π.

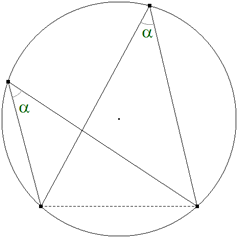
figura 4

TEOREMA 1.6 Angulos de la misma cuerda son iguales.

figura 5

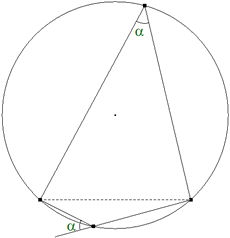
TEOREMA 1.7 El ángulo entre cuerda y tangente es igual al ángulo de la cuerda

figura 6

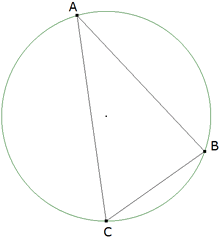
TEOREMA 1.8 El ángulo exterior de un cuadrilátero inscrito en un círculo es igual al ángulo interior opuesto

figura 7

figura 8

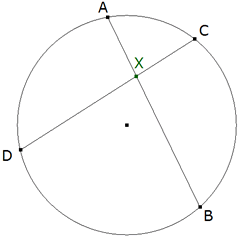
TEOREMA 1.9 XA.XB = XC.XD

figura 9

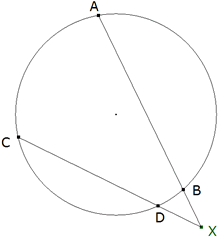
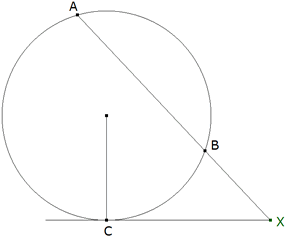
TEOREMA 1.10 XA.XB = XC²

figura 10

Gracias al TEOREMA 1.5, sabemos trazar las tangentes desde un punto a una circunferencia.

figura 11

Y por último, también sabemos trazar el círculo por tres puntos.

2. TEOREMAS PREVIOS CON DEMOSTRACION

En este apartado, demostramos siete teoremas que junto a la observación detenida de las figuras constituyen las herramientas básicas para hallar la solución que buscamos.

TEOREMA 2.1 (centro radical)

Dados tres círculos, las cuerdas comunes a dos de ellos se encuentran en un mismo punto. Este punto recibe el nombre de centro radical.

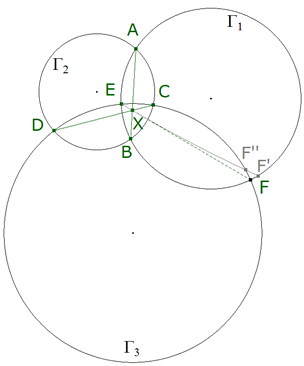
figura 12

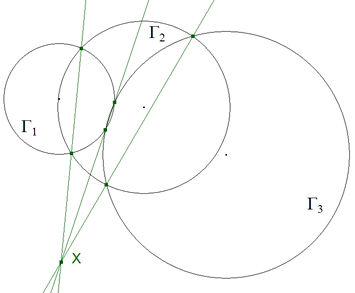
DEMOSTRACION 2.1

Γ₁ y Γ₂ se cortan en A y B, Γ₂ y Γ₃ se cortan en C y D, Γ₃ y Γ₁ se cortan en E y F. AB y CD se cortan en X y EX corta a Γ₁ en F’ y a Γ₃ en F”. Entonces aplicando el TEOREMA 1.9:

como cuerdas de Γ₁ XE.XF’ = XA.XB

como cuerdas de Γ₂ XA.XB = XC.XD

como cuerdas de Γ₃ XC.XD = XE.XF”

de donde XE.XF’ = XE.XF” y por tanto F’ = F” = F con lo que EF pasa también por X.

Concluimos pues que AB, CD y EF son concurrentes.

DISTINTAS CONFIGURACIONES DEL CENTRO RADICAL

figura 13

En este caso, el centro radical es exterior a los círculos.

figura 14

En este caso el centro radical es impropio

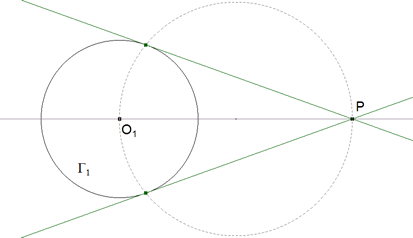
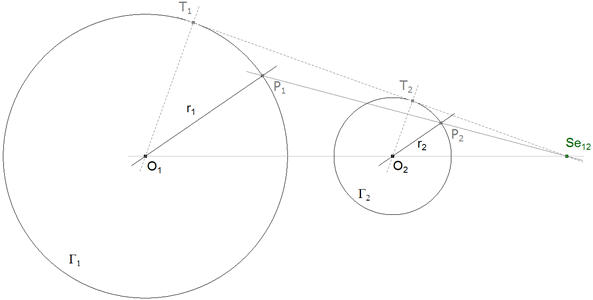
TEOREMA 2.2 (centro de semejanza externo)

La recta P₁P₂ que une los extremos de dos radios, paralelos y en el mismo sentido, de dos círculos Γ₁ y Γ₂ pasa por un punto fijo Se₁₂. Este punto está situado en la prolongación de la línea de centros.

figura 15

DEMOSTRACION 2.2

Observando la figura, vemos que los radios O₁P₁, O₂P₂ son paralelos y de según los TEOREMAS 1.1 a 1.4

O₁P₁/O₂P₂= Se₁₂O₁/Se₁₂O₂ = r₁/r₂ y de aquí (r₁-r₂)/r₂= O₁O₂/Se₁₂O₂

como O₁O₂ es constante, se deduce que Se₁₂O₂ también es constante y Se₁₂ fijo.

COROLARIO 2.2

Cuando es posible trazar la tangente exterior T₁T₂ común a Γ₁ y Γ₂, esta tangente pasa necesariamente por Se₁₂. Como O₁T₁ y O₂T₂ son perpendiculares a una misma recta T₁T₂, son paralelas entre sí.

Se₁₂ es denominado centro de semejanza externo porque divide a O₁O₂ externamente según la razón de los radios r₁/r₂.

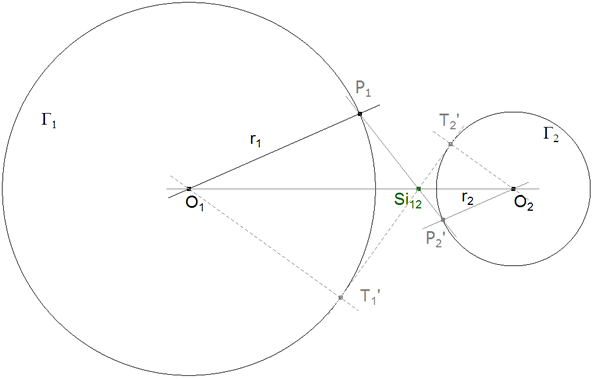
TEOREMA 2.3 (centro de semejanza interno)

La recta P₁P₂' que une los extremos de dos radios, paralelos y en sentido opuesto, de dos círculos Γ₁ y Γ₂ pasa por un punto fijo Si₁₂. Este punto está situado entre los dos centros y sobre la prolongación de la línea de centros.

figura 16

DEMOSTRACION 2.3

Al igual que en 2.2, los dos triángulos semejantes O₁P₁Si₁₂, O₂P₂'Si₁₂ dan las siguientes proporciones

r₁/r₂ = O₁Si₁₂/O₂Si₁₂ y de aquí (r₁+r₂)/r₁= O₁O₂/O₂Si₁₂

como O₁O₂ es constante, se deduce que Se₁₂O₂ también es constante y Si₁₂ fijo.

COROLARIO 2.3

Se concluye que, cuando es posible trazar la tangente interior T₁T₂' común a Γ₁ y Γ₂, esta tangente pasa necesariamente por Si₁₂. Como O₁T₁' y O₂T₂' son paralelas entre ellas por ser perpendiculares a una misma recta T₁'T₂' y de sentido contrario.

Si₁₂ es denominado centro de semejanza interno porque divide a O₁O₂ internamente según la razón de los radios r₁/r₂.

CONFIGURACIONES SINGULARES DEL CENTRO DE SEMEJANZA

figura 17

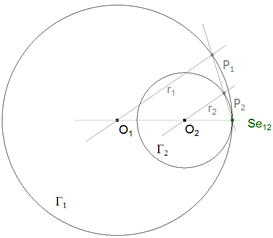
La tangencia interior de los círculos proporciona el centro de semejanza exterior en el punto de tangencia.

figura 18

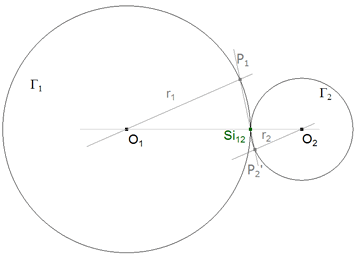
La tangencia exterior de los círculos proporciona el centro de semejanza interior en el punto de tangencia.

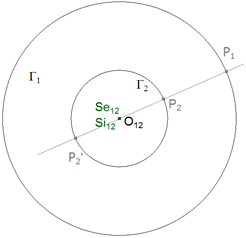
figura 19

En círculos concéntricos, los dos centros de semejanza coinciden en el centro de los círculos.

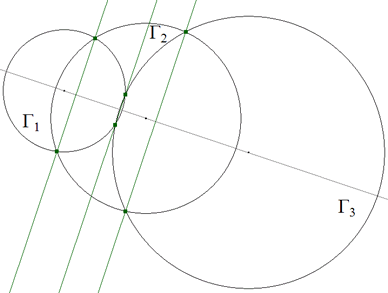
TEOREMA 2.4 (eje de semejanza de los centros exteriores)

Dados tres círculos, los centros de semejanza exteriores de cada par de círculos están alineados en una misma recta.

figura 20

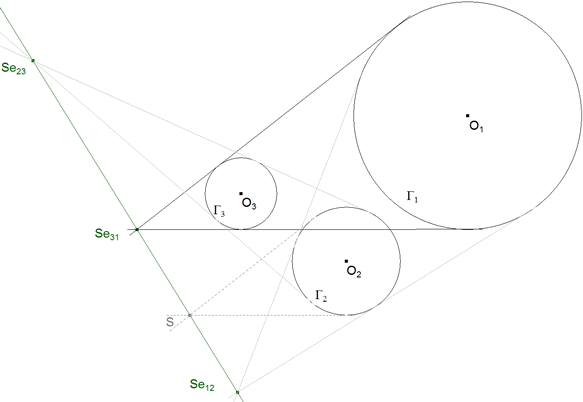
DEMOSTRACION 2.4

Con la observación detenida de la figura y teniendo presente el TEOREMA 1.4 podemos abordar la demostración.

Sean Γ₁, Γ₂ y Γ₃ los círculos. Sean Se₁₂, Se₂₃ y Se₃₁ los centros de semejanza externos correspondientes. Trazamos por Γ₂ dos tangentes paralelas a las tangentes exteriores y comunes a Γ₃ y Γ₁; estas tangentes se cortan en S. Consideramos ahora la semejanza de los círculos Γ₁ y Γ₂; Se₃₁ y S son puntos homólogos y como tales tienen que estar alineados con el centro de semejanza Se₁₂. Si tomamos ahora la semejanza de los círculos Γ₂ y Γ₃; Se₃₁ y S son igualmente puntos homólogos y como tales tienen que estar alineados con el centro de semejanza Se₂₃.

Resulta entonces que Se₁₂, Se₂₃ y Se₃₁ están en una misma recta.

TEOREMA 2.5 (eje de semejanza de dos centros interiores y un centro exterior)

Dados tres círculos, los centros de semejanza interiores de dos pares de círculos están sobre una misma recta con el centro de semejanza exterior del tercer par de círculos.

figura 21

DEMOSTRACION 2.5

De forma parecida a 2.4; sean Γ₁, Γ₂ y Γ₃ los círculos. Sean Se₁₂, Si₂₃ y Si₃₁ el centro externo y los dos centros de semejanza internos correspondientes. Tracemos por Γ₂ dos tangentes paralelas a las tangentes interiores y comunes a Γ₃ y Γ₁; estas tangentes se cortan en S. Consideremos ahora la semejanza de los círculos Γ₁ y Γ₂; Si₃₁ y S son puntos homólogos y como tales tienen que estar alineados con el centro de semejanza Se₁₂. Si tomamos ahora la semejanza de los círculos Γ₂ y Γ₃; Si₃₁ y S son igualmente puntos homólogos y como tales tienen que estar alineados con el centro de semejanza Si₃₁.

Resulta entonces que Se₁₂, Si₂₃ y Si₃₁ están en una misma recta.

Lo mismo hallaríamos para Si₁₂, Se₂₃ y Si₃₁ y para Si₁₂, Si₂₃ y Se₃₁.

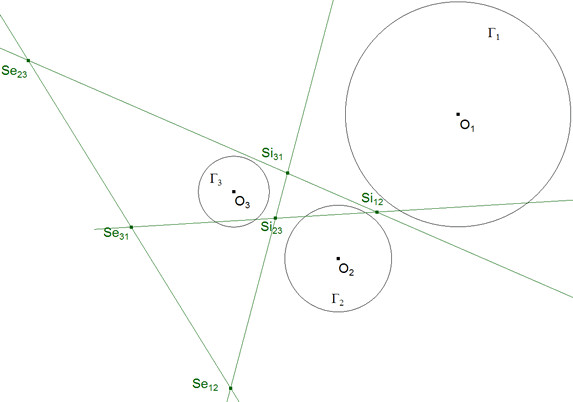
LOS CUATRO EJES DE SEMEJANZA DE UN SISTEMA DE TRES CÍRCULOS

figura 22

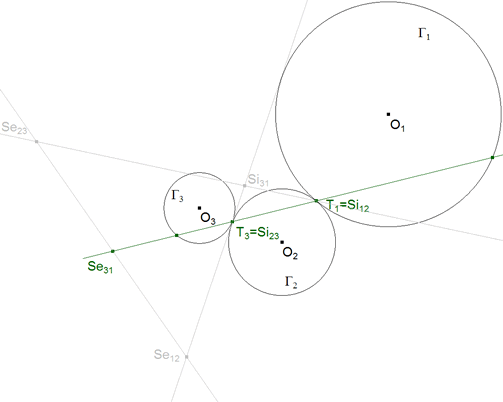
TEOREMA 2.6

Si un círculo Γ₂ es tangente en T₁ a un círculo Γ₁ y en T₃ a un círculo, Γ_3, la recta T₂T₃ pasa por uno de los centros de semejanza de los dos círculos Γ_1,Γ_3.

figura 23

DEMOSTRACION 2.6

Teniendo en cuenta los TEOREMAS 2.2 a 2.5 y en especial las configuraciones singulares en los casos de tangencia de los centros de semejanza (figuras 17 y 18),

el punto T₁ es Si₁₂, centro de semejanza interior de Γ₁ y Γ₂,

el punto T₃ es Si₂₃, centro de semejanza interior de Γ₂ y Γ₃.

Como hemos visto en el TEOREMA 2.5 estarán en la misma recta que el centro de semejanza exterior Se₃₁.

NOTA 2.6

Si el círculo es tangente de la misma manera a los otros dos, es decir toca a los dos interiormente o toca a los dos exteriormente, la recta pasa por el centro de semejanza exterior; si por el contrario, es tangente de forma diferente, la recta pasa por el centro de semejanza interior.

REGLA 2.6

DADO T₁, T₃ES EL PUNTO NO SEMEJANTE A T₁ DE LOS DOS EN QUE T₃T₁ CORTA AL CIRCULO Γ₃ (figura 23).

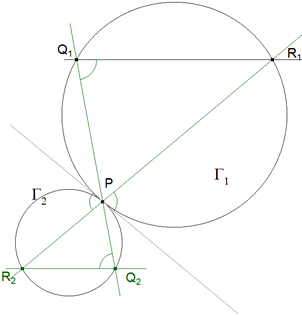
TEOREMA 2.7

Dado un círculo Γ₁ por tres puntos PQ₁R₁ y un segundo círculo Γ₂ tangente al primero en P, Q₁P y R₁P encuentran a Γ₂, además de en P, en Q₂ y R₂ respectivamente. Entonces Q₁R₁ es paralela a Q₂R₂.

figura 24

DEMOSTRACION 2.7

Si consideramos la tangente común por P, basta aplicar los TEOREMAS 1.1 a 1.3 y el TEOREMA 1.7 para deducir la igualdad de ángulos y con ello el paralelismo de las rectas Q₁R₁ y Q₂R₂.

3. IDENTIFICACION DEL PROBLEMA DE CASTILLON EQUIVALENTE

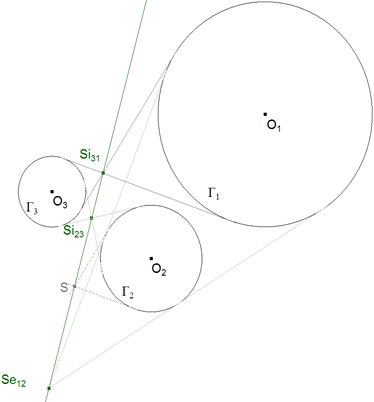
Suponemos ahora que el problema está resuelto y estudiamos la figura resultante (figura 25). Empezamos por el caso en el que los tipos de las tres tangencias coinciden (todas externas o todas internas); en este caso nos fijamos en el eje de semejanza externo.

En el caso de tangencias distintas, vamos a trabajar con los ejes de semejanza internos; pero el procedimiento es idéntico .

3.1 UN ENUNCIADO EQUIVALENTE PREVIO.

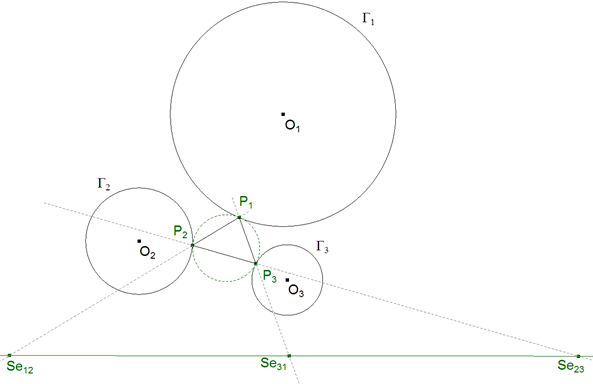
figura 25

ENUNCIADO ORIGINAL

Trazar el círculo tangente a tres círculos dados Γ₁, Γ₂ y Γ₃.

ENUNCIADO EQUIVALENTE PREVIO

Hallar los puntos de contacto P₁, P₂ y P₃.

Si construimos el eje de semejanza por Se₁₂, Se₂₃ y Se₃₁ y utilizamos el TEOREMA 2.6,

P₁P₂pasa por Se₁₂,

P₂ P₃ asa por Se₂₃,

P₃P₁ pasa por Se₃₁.

En este momento, sabemos por que puntos conocidos pasan las distintas rectas que forman los puntos de contacto; pero no conocemos los puntos de contacto en absoluto y, por supuesto, tampoco conocemos el círculo que definen (que es la solución).

Para paliar esta situación, intentaremos trabajar en uno de los círculos dados (que sí es conocido por nosotros) y para ello profundizaremos en la observación de la figura anterior, mejorándola (figura 26).

3.2 BÚSQUEDA DE PUNTOS AUXILIARES CONOCIDOS.

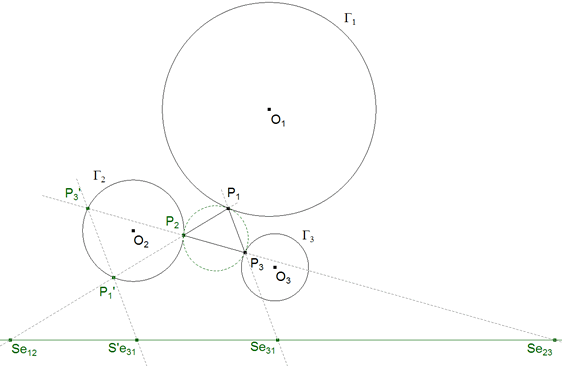
figura 26

Observando la figura, establecemos que

P₁P₂ vuelve a cortar a Γ₂ en P₁',

P₂P₃ vuelve a cortar a Γ₂ en P₃',

P₃'P₁' corta al eje de semejanza Se₁₂Se₂₃ en S’e₃₁.

Vemos que es suficiente determinar los puntos P₁'P₂P₃' en Γ₂ y además

P₂P₃' corta al eje de semejanza en Se₂₃

P₁'P₂ corta al eje de semejanza en Se₁₂

P₃'P₁' corta al eje de semejanza en S’e₃₁

Conocemos Se₁₂ y Se₂₃; pero ¿podemos establecer S’e₃₁?. Lo vemos en la figura 27.

3.3 DETERMINACIÓN DEL PUNTO AUXILIAR S’e₃₁.

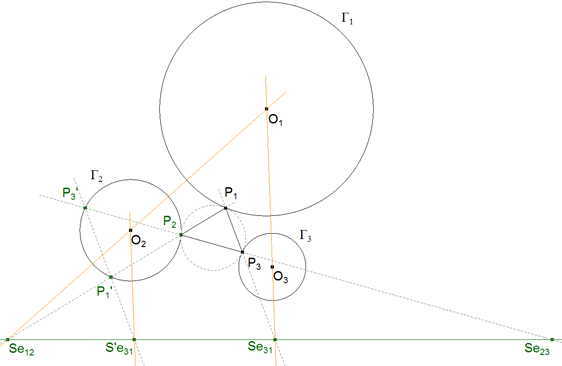
figura 27

Podemos decir (TEOREMA 2.7) que P₃P₁ y P₃'P₁' son paralelas; entonces el triángulo Se₁₂Se₃₁O₁ y el triángulo Se₁₂S’e₃₁O₂ son semejantes. Si r₁ y r₂ son los radios de Γ₁ y Γ₂

Se₁₂Se₃₁/Se₁₂S’e₃₁= Se₁₂P₁/Se₁₂P₁' = r₁/r₂

y si O₁ y O₂ son los centros respectivos de Γ₁ y Γ₂

Se₁₂O₁/Se₁₂O₂ = r₁/r₂

podemos pues decir que el triángulo Se₁₂O₁Se₃₁ y el triángulo Se₁₂O₂S’e₃₁ son semejantes y en consecuencia O₁O₃ y O₂S’e₃₁ son paralelas.

Concluimos que para obtener el punto auxiliar S’e₃₁, trazamos por O₂ una paralela a O₁O₃; esta paralela cortará al eje de semejanza en el punto buscado.

3.4 EL PROBLEMA DE CASTILLON EQUIVALENTE AL PROBLEMA DE APOLONIO.

Vemos que el problema que nos queda es el siguiente:

“ Dado un círculo Γ₂ y tres puntos alineados Se₁₂, S’e₃₁y Se₂₃; inscribir un triángulo en el círculo de forma que sus lados pasen por cada uno de los puntos dados. ”

¡ NO ES MAS QUE EL PROBLEMA DE CASTILLON, EN QUE LOS TRES PUNTOS DADOS ESTAN ALINEADOS !

4. SOLUCION DEL PROBLEMA DE CASTILLON PARA PUNTOS ALINEADOS

Del problema de Castillon con los tres puntos alineados podemos decir que es el primer caso del problema de Castillon resuelto en la historia de la Geometría y fue resuelto por Pappus.

Este problema puede ser resuelto por muchos de los métodos generales que hoy en día se conocen; pero dada la singularidad en la distribución de los tres puntos dados (alineados), explicitámos la solución particular de este caso.

Esta solución es sencilla y usa, sólo, conocimientos de Geometría Clásica, como en su día hizo Pappus.

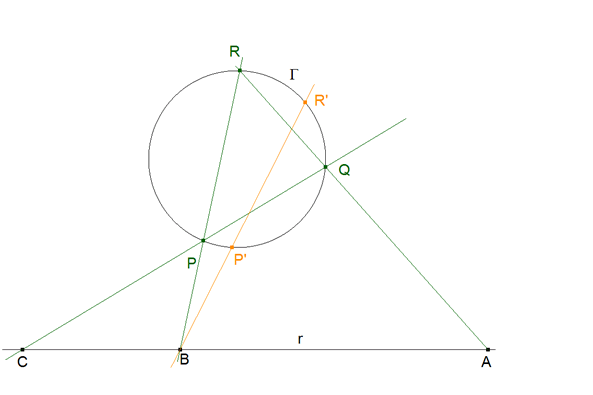
ENUNCIADO DEL PROBLEMA EQUIVALENTE SOBRE EL PROBLEMA ORIGINAL

figura 28

Dado un círculo Γ y tres puntos A, B, C sobre una recta r, inscribir un triángulo PQR en Γ de forma que QR pase por A, RP pase por B y PQ pase por C*.

*Aislamos el problema equivalente del problema original haciendo el siguiente cambio de notación (Se₂₃, S’e₃₁, Se₁₂, P₁', P₂, P₃', Γ₂) son en este apartado (A, B, C, P, Q, R, Γ)

SOLUCION DEL PROBLEMA DE CASTILLON PARA PUNTOS ALINEADOS

4.1 PASO 1 (UNA PROPIEDAD DEL CIRCULO)

Suponemos el problema resuelto

figura 29

Suponemos también una segunda recta por B que corta a Γ en P’ y R’. Podemos escribir (TEOREMA 1.9)

BP.BR=BP’.BR’

SOLUCION DEL PROBLEMA DE CASTILLON PARA PUNTOS ALINEADOS

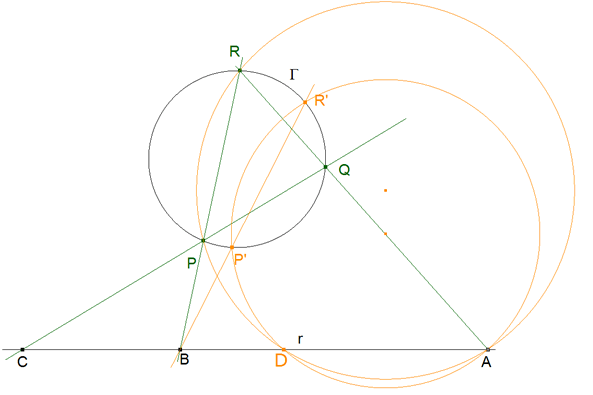
4.2 PASO 2 (DETERMINACION DEL PRIMER PUNTO AUXILIAR D)

figura 30

Trazamos ahora el círculo por P, R y A y recuperamos el TEOREMA 1.9. Este círculo corta a r en D y por tanto se cumple

BP.BR=BD.BA

Trazamos también el círculo por P’, R’ y A. Este círculo corta a r en D’, entonces se cumple

BP’.BR’=BD’.BA

pero hemos visto (4.1) que

BP.BR=BP’.BR’

y por tanto

BD.BA=BD’.BA

de donde

BD=BD’ y D=D’

B es el centro radical de los tres círculos (TEOREMA 2.1).

Vemos que D es fijo y que todos los círculos, trazados como los anteriores, cortan a r en D.

Aunque no conocemos P y R, si cortamos Γ por cualquier recta por B nos da P’ y R’. El círculo por P’, R’ y A nos da D en su intersección con r.

Se puede comprobar que si DP vuelve a cortar a Γ en G, entonces GQ es paralela a r.

Conocemos A, B, C, y D; pero no sabemos todavía nada de P, Q y R.

Trazamos ahora el mismo tipo de círculos por P, Q y D

SOLUCION DEL PROBLEMA DE CASTILLON PARA PUNTOS ALINEADOS

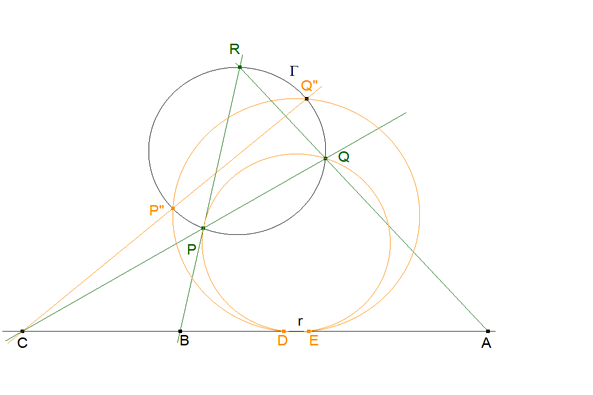
4.3 PASO 3 (DETERMINACION DEL SEGUNDO PUNTO AUXILIAR E)

figura 31

Una recta por C Corta Γ en P” y Q”. Trazamos ahora el círculo por P,Q y D.

Este círculo corta a r en E y por tanto se cumple (TEOREMA 1.9)

CP.CQ=CD.CE

Tracemos también el círculo por P”, Q” y D.

Supongamos que este círculo corta a r en E”, entonces se cumpliría

CP”.CQ”=CD.CE”

pero en el círculo Γ (TEOREMA 1.9)

CP.CQ=CP”.CQ”

y por tanto

CD.CE=CD.CE”

de donde

CE=CE” y E=E”

C es el centro radical de los tres círculos (TEOREMA 2.1).

Vemos que E es fijo y que todos los círculos trazados como los anteriores cortan a r en E.

Aunque no conocemos P y Q, cortando Γ por cualquier recta por C nos da P” y Q”. El círculo por P”, Q” y D nos da E en su intersección con r.

Conocemos A, B, C, D y E; pero no sabemos todavía nada de P, Q y R.

Pasamos a vincular ahora los puntos auxiliares D y E con el punto Q (solución).

SOLUCION DEL PROBLEMA DE CASTILLON PARA PUNTOS ALINEADOS

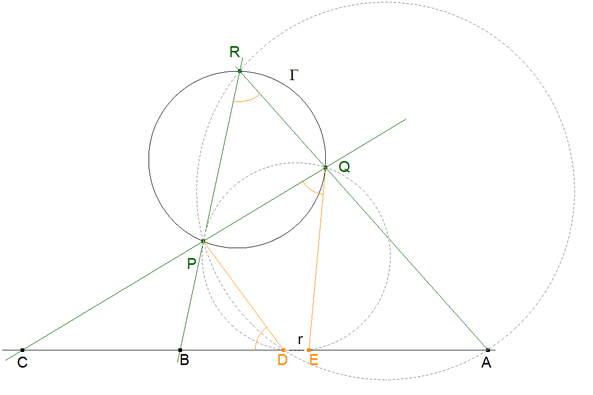
4.4 PASO 4 (Y ULTIMO, DETERMINACION DE Q)

figura 32

En el círculo por P, R, A y D, se cumple la igualdad de ángulos vista en el TEOREMA 1.8

∠PRA=∠PDB

En el círculo por P, Q, E y D, se cumple la igualdad de ángulos vista en el TEOREMA 1.8

∠PQE=∠PDB

y como ∠PRA=∠PRQ, deducimos

∠PQE=∠PRQ

entrando con esta igualdad de ángulos en el TEOREMA 1.7 deducimos que QE es la tangente al círculo Γ en el punto Q.

Como conocemos la posición de E, podemos trazar desde E la tangente a Γ. El punto de contacto es Q, entonces QA nos da R en su intersección con Γ y QC nos da, del mismo modo, P.

Hemos obtenido P, Q y R.

Pero desde E, puede trazarse otra tangente al círculo y por lo tanto hallamos otra solución

SOLUCION DEL PROBLEMA DE CASTILLON PARA PUNTOS ALINEADOS

4.5 SEGUNDA SOLUCION

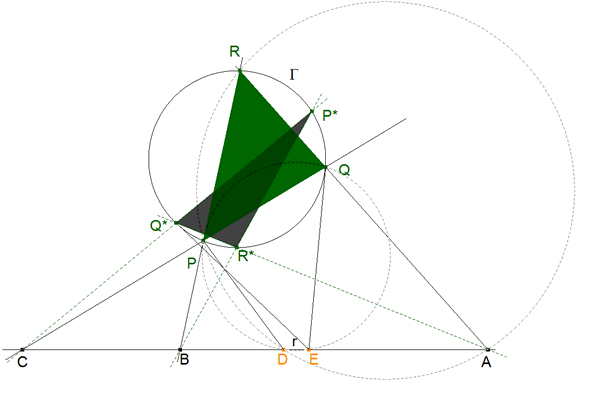
figura 33

Como conocemos la posición de E, podemos trazar, desde E, otra tangente a Γ. El punto de contacto es Q*, entonces Q*A nos da R* en su intersección con Γ y Q*C nos da, del mismo modo, P*.

5. PROBLEMA DE APOLONIO DETERMINACION DE LOS PUNTOS DE CONTACTO

Debemos ahora utilizar cuatro veces la solución obtenida en el Problema de Castillon para obtener todas las soluciones del Problema de Apolonio.

Una vez para cada eje de semejanza y dos soluciones por eje nos proporciona las ocho soluciones que tiene, en general, el problema.

5.3 y 5.4 son una mera repetición del punto 5.2, aunque en 5.3 usamos puntos distintos y en 5.4 un círculo distinto.

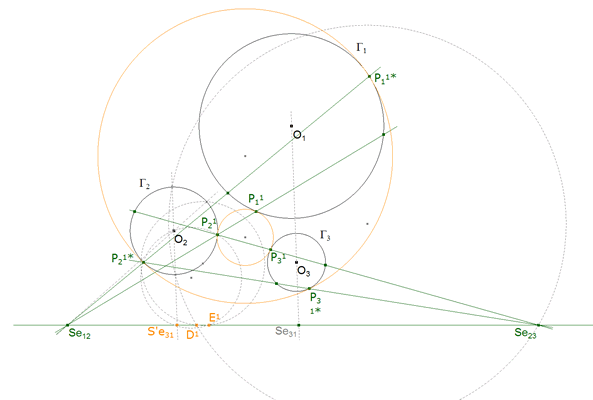
5.1 EJE Se_12,Se_23,Se₃₁ Y PUNTOS DE CONTACTO (P₁¹, P₂¹, P₃¹) y (P₁¹*, P₂¹*, P₃¹*).

figura 34

a Trabajamos con Γ₂. Por O₂ paralela a O₃O₁ que corta al eje en S’e₃₁.

b Aprovechamos la paralela por O₂ que nos proporciona dos intersecciones con Γ₂.

c Círculo por esos dos puntos y Se₂₃ (ó Se₁₂) que corta al eje en D¹.

d Recta por O₂ desde Se₁₂ (ó Se₂₃) que nos da dos intersecciones con Γ₂.

e Círculo por esos dos puntos y D¹ que corta al eje en E¹.

f Puntos de contacto P₂¹ y P₂¹* de las tangentes desde E¹ a Γ₂.

g P₂¹Se₁₂ tiene dos intersecciones con Γ₁, P₁¹ es el NO semejante a P₂¹ REGLA 2.6.

h P₂¹Se₂₃ tiene dos intersecciones con Γ₃, P₃¹ es el NO semejante a P₂¹.

i P₂¹*Se₁₂ tiene dos intersecciones con Γ₁, P₁¹* es el NO semejante a P₂¹*.

j P₂¹*Se₂₃ tiene dos intersecciones con Γ₃, P₃¹* es el NO semejante a P₂¹*.

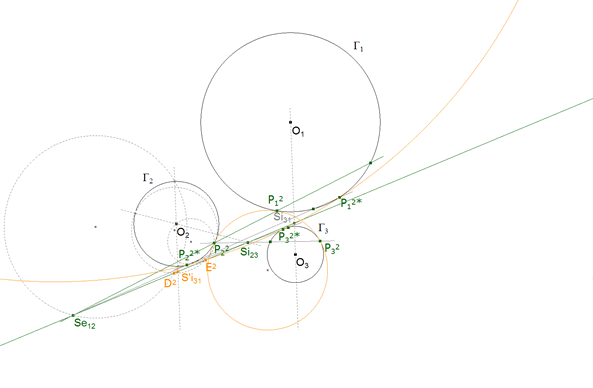
5.2 EJE Se_12,Si_23,Si₃₁ Y PUNTOS DE CONTACTO (P₁², P₂², P₃²) y (P₁²*, P₂²*, P₃²*).

figura 35

a Trabajamos con Γ₂. Por O₂ paralela a O₃O₁ que corta al eje en S’i₃₁.

b Aprovechamos la paralela por O₂ que nos proporciona dos intersecciones con Γ₂.

c Círculo por esos dos puntos y Se₁₂ (ó Si₂₃) que corta al eje en D².

d Recta por O₂ desde Si₂₃ (ó Se₁₂) que nos da dos intersecciones con Γ₂.

e Círculo por esos dos puntos y D² que corta al eje en E².

f Puntos de contacto P₂² y P₂²* de las tangentes desde E² a Γ₂.

g P₂²Se₁₂ tiene dos intersecciones con Γ₁, P₁² es el NO semejante a P₂² REGLA 2.6.

h P₂²Si₂₃ tiene dos intersecciones con Γ₃, P₃² es el NO semejante a P₂².

i P₂²*Se₁₂ tiene dos intersecciones con Γ₁, P₁²* es el NO semejante a P₂²*.

j P₂²*Si₂₃ tiene dos intersecciones con Γ₃, P₃²* es el NO semejante a P₂²*.

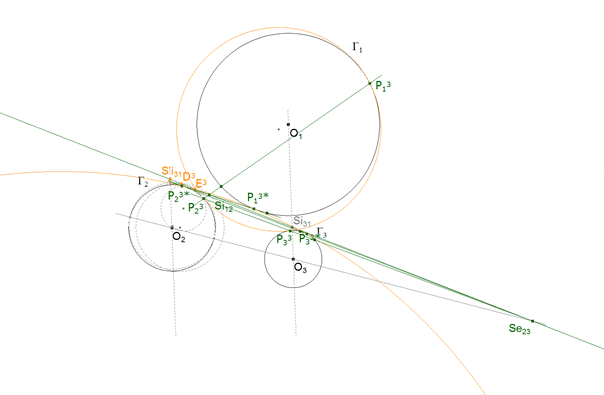
5.3 EJE Si_12,Se_23,Si₃₁ Y PUNTOS DE CONTACTO (P₁³, P₂³, P₃³) y (P₁³*, P₂³*, P₃³*).

figura 36

a Trabajamos con Γ₂. Por O₂ paralela a O₃O₁ que corta al eje en S’i₃₁.

b Aprovechamos la paralela por O₂ que nos proporciona dos intersecciones con Γ₂.

c Círculo por esos dos puntos y Si₁₂ (ó Se₂₃) que corta al eje en D³.

d Recta por O₂ desde Se₂₃ (ó Si₁₂) que nos da dos intersecciones con Γ₂.

e Círculo por esos dos puntos y D³ que corta al eje en E³.

f Puntos de contacto P₂³ y P₂³* de las tangentes desde E³ a Γ₂.

g P₂³Si₁₂ tiene dos intersecciones con Γ₁, P₁³ es el NO semejante a P₂³ REGLA 2.6.

h P₂³Se₂₃ tiene dos intersecciones con Γ₃, P₃³ es el NO semejante a P₂³.

i P₂³*Si₁₂ tiene dos intersecciones con Γ₁, P₁³* es el NO semejante a P₂³*.

j P₂³*Se₂₃ tiene dos intersecciones con Γ₃, P₃³* es el No semejante a P₂³*.

5.4 EJE Si_12,Si_23,S2₃₁ Y PUNTOS DE CONTACTO (P₁³, P₂⁴, P₃⁴) y (P₁⁴*, P₂⁴*, P₃⁴*).

figura 37

a Trabajamos con Γ₃. Por O₃ paralela a O₁O₂ que corta al eje en S’i₁₂.

b Aprovechamos la paralela por O₃ que nos proporciona dos intersecciones con Γ₃.

c Círculo por esos dos puntos y Se₃₁ (ó Si₂₃) que corta al eje en D⁴.

d Recta por O₃ desde Si₂₃ (ó Se₃₁) que nos da dos intersecciones con Γ₃.

e Círculo por esos dos puntos y D⁴ que corta al eje en E⁴.

f Puntos de contacto P₃⁴ y P₂³* de las tangentes desde E⁴ a Γ₃.

g P₃⁴Se₃₁ tiene dos intersecciones con Γ₁, P₁⁴ es el NO semejante a P₃⁴ REGLA 2.6.

h P₃⁴Si₂₃ tiene dos intersecciones con Γ₂, P₂⁴ es el NO semejante a P₃⁴.

i P₃⁴*Se₃₁ tiene dos intersecciones con Γ₁, P₁⁴* es el NO semejante a P₃⁴*.

j P₃⁴*Si₂₃ tiene dos intersecciones con Γ₂, P₂⁴* es el No semejante a P₃⁴*.

LAS OCHO SOLUCIONES

figura 38