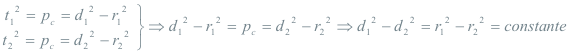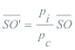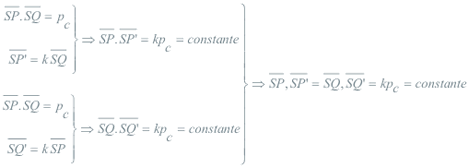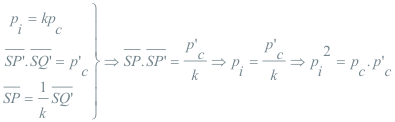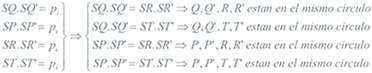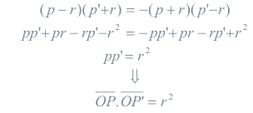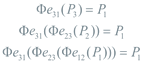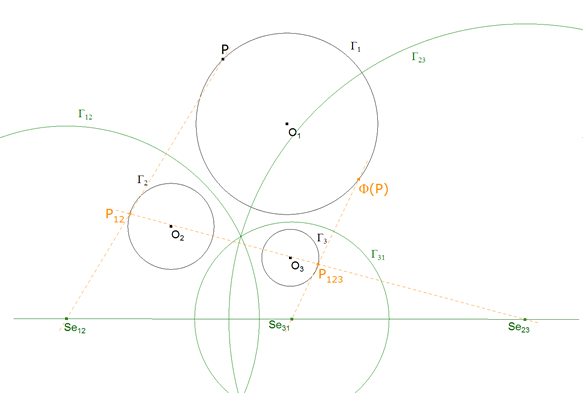EL PROBLEMA DE APOLONIO Y EL PROBLEMA DE CASTILLON José María Pedret. Ingeniero Naval. Esplugues de Llobregat (Barcelona).

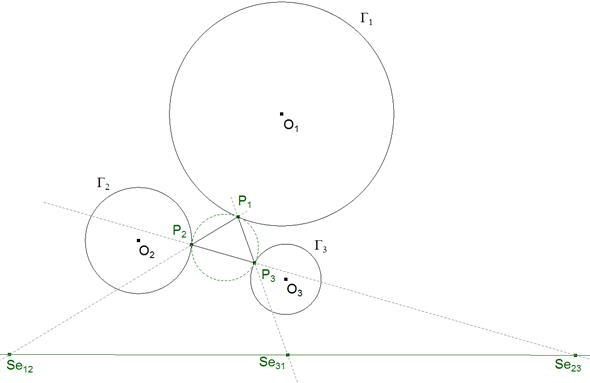
TRAZAR EL CÍRCULO TANGENTE A TRES CÍRCULOS DADOS. No parece, éste, el problema más adecuado para una revista especializada en triángulos; pero si transformamos el problema de buscar el círculo tangente por el problema de buscar el triángulo que pasa por los puntos de contacto ya habremos dado un paso hacia el mundo de los triángulos. Se objetará que los puntos de contacto no se conocen; pero si estudiamos la figura propuesta, podemos, de nuevo, encontrar un triángulo vinculado al anterior cuyos lados pasan por tres puntos conocidos y está inscrito en uno de los círculos dados. JULIUS PETERSEN en su obra Métodos y teorías para la resolución de problemas de construcciones geométricas propone el problema de Apolonio como problema 403 y aunque no es el método que desarrolla, indica lo siguiente: 403. TRAZAR UN CIRCULO TANGENTE A TRES CIRCULOS DADOS ...Se puede también resolver por un procedimiento que es completamente igual al que se aplica al problema 201. El triángulo que se trata de construir es aquel cuyos vértices coinciden con los puntos de contacto buscados; sus lados pasan por tres de los centros de similitud de los círculos dados. Si tomamos esos puntos como centros de inversión eligiendo las potencias de inversión de tal manera que dos cualesquiera de los círculos se intercambian entre ellos, cada uno de los círculos después de tres inversiones volverá a la posición inicial. No hay pues diferencia esencial entre el problema que nos ocupa y el que ya ha sido resuelto anteriormente... El problema 201 en el libro de Petersen corresponde al problema de Castillon

Resolvamos el problema de Apolonio: TRAZAR UN CIRCULO TANGENTE A TRES CIRCULOS DADOS Primero Pasar del problema de Apolonio al problema de Castillon Segundo Aplicación a resolver el problema original de Apolonio

0. INTRODUCCION	solución 2

Para pasar del Problema de Apolonio al Problema de Castillon dice PETERSEN ... EL TRIÁNGULO QUE SE TRATA DE CONSTRUIR ES AQUEL CUYOS VÉRTICES COINCIDEN CON LOS PUNTOS DE CONTACTO BUSCADOS; SUS LADOS PASAN POR TRES DE LOS CENTROS DE SIMILITUD DE LOS CÍRCULOS DADOS. SI TOMAMOS ESOS PUNTOS COMO CENTROS DE INVERSIÓN ELIGIENDO LAS POTENCIAS DE INVERSIÓN DE TAL MANERA QUE DOS CUALESQUIERA DE LOS CÍRCULOS SE INTERCAMBIAN ENTRE ELLOS, CADA UNO DE LOS CÍRCULOS DESPUÉS DE TRES INVERSIONES VOLVERÁ A LA POSICIÓN INICIAL ... De la lectura detenida de la indicación anterior, está claro que tenemos que saber INTERCAMBIAR DOS CIRCULOS POR MEDIO DE UNA INVERSION y por ello empezamos el apartado uno definiendo la inversión y viendo como se invierten rectas y círculos. Acabaremos las ideas sobre inversión viendo las relaciones entre dos círculos para poder considerarlos como figuras inversas. Inversión y semejanza son equivalentes; pero sólo para los puntos sobre la circunferencia. Todas las ideas sobre centros y ejes de semejanza entre círculos se encuentran en la primera solución. A lo largo del documento, podemos sustituir la palabra semejanza por homotecia. En el apartado dos, vemos también la realización de las construcciones típicas de la geometría inversiva mediante el uso de la regla y compás. En el apartado tres reconocemos el Problema de Castillon equivalente con la ayuda del TEOREMA 3.1 (que ya vimos en la primera solución) sobre la alineación de los puntos de contacto. Realmente es el método de resolución del Problema de Castillon el que nos interesa; pero aquí no conocemos el círculo del problema. Por eso veremos como se transforman los puntos de las circunferencias de nuestro problema si seguimos las ideas de PETERSEN. Entramos en el apartado cuatro para establecer el comportamiento de los puntos de contacto durante la composición de las tres inversiones que intercambian los círculos dos a dos. Los puntos de contacto son fijos en la transformación señalada. En el apartado cinco estudiamos el comportamiento de un punto cualquiera en la composición de las tres inversiones. Para atacar el TEOREMA 5.3, hay que prestar mucha atención a los TEOREMAS 1.8 Y 1.9 porque son los que nos han permitido vincular la inversión que intercambia dos círculos con la restricción a esos círculos de una homología del plano. La homología es homografía. Las tres inversiones serán pues composición de tres homografías del plano. Como la composición de homografías es homografía, HEMOS IDENTIFICADO LA SUCESIÓN DE INVERSIONES QUE MENCIONA PETERSEN CON UNA HOMOGRAFÍA DEL CÍRCULO SOBRE SÍ MISMO. Si los puntos de contacto son fijos, están en la intersección del círculo y el eje de la homografía del círculo sobre sí mismo. De aquí desgranamos el método de solución en el apartado seis.

1. LA INVERSION	solución 2

Incluimos en este apartado nueve definiciones y teoremas que nos permiten fijar las ideas de inversión mínimas para poder atacar este problema.

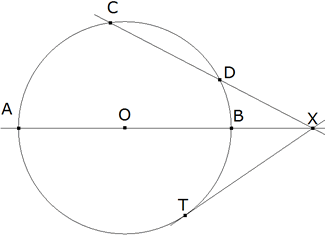
1.1 POTENCIA DE UN PUNTO RESPECTO A UN CIRCULO figura 1 De la primera solución recordamos el TEOREMA 1.9 que es además la condicón para que los puntos A, B, C, D estén en el mísmo círculo (dichos puntos se denominan cocíclicos). Sea un círculo de centro O y radio r y sea X un punto exterior a él, p_c recibe el nombre de potencia del punto X respecto al círculo. A y B son los puntos de intersección del círculo y OX. Tomamos O como origen y OX como eje de abscisas; si OX=d, OA=-r y OB=r

TEOREMA 1.2 (EJE RADICAL DE DOS CIRCULOS) El lugar de los puntos, cuyos cuadrados de las distancias a dos puntos fijos tienen una diferencia constante a², es una recta perpendicular a la recta que une los dos puntos fijos.

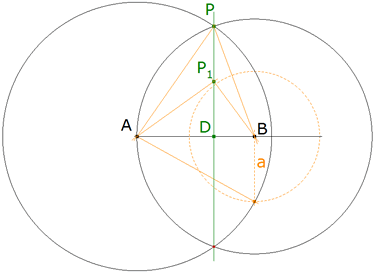
DEMOSTRACION 1.2 Sean A y B los puntos fijos, P uno de los puntos del lugar, PD una perpendicular a AB. Todo punto de BD poseerá la propiedad requerida; tomemos, por ejemplo, P; tenemos: figura 2 Construimos un triángulo rectángulo siendo uno de sus catetos a, sean A y B los centros des los círculos cuyos radios son respectivamente iguales a la hipotenusa y al otro cateto del triángulo, la recta buscada pasa por los puntos de intersección de estos dos círculos (Hemos supuesto P más alejado de A que de B). COROLARIO 1.2 (EJE RADICAL) Como hemos visto en 1.1 la potencia de un punto puede expresarse como el cuadrado de la tangente o como la diferencia entre el cuadrado de la distancia al centro y el cuadrado del radio. Si la tangente al primer círculo es t₁ y la tangente al segundo círculo es t₂ y queremos ver que puntos cumplen con la igualdad de tangentes a dos círculos distintos: El lugar geométrico de los puntos desde donde pueden trazarse tangentes iguales a dos círculos (o que tienen la misma potencia respecto a dos círculos) es una recta perpendicular a la recta que une los centros (eje radical, eje de igual potencia de los círculos). Sólo necesitamos aplicar el teorema que acabamos de demostrar. Cuando los círculos se cortan, el eje radical pasa por sus puntos de intersección. Los tres ejes radicales de tres círculos pasan por el mismo punto (primera solución TEOREMA 2.1), el punto de igual potencia o centro radical. Gracias a esto, determinamos fácilmente el eje radical de dos círculos que no se cortan; basta trazar un círculo cualquiera que corte a los dos primeros.

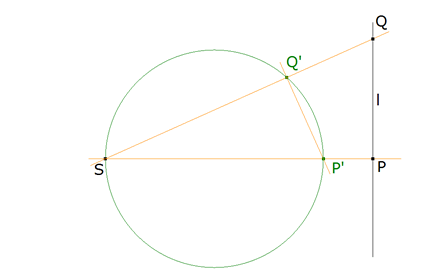
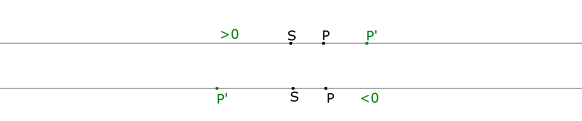
1.3 INVERSION figura 3 Sea un punto fijo S y un número p_i, positivo (o negativo), se llama inversión de polo (centro) S y potencia p_i a la transformación en la que a cada punto P del plano (o del espacio) hace corresponder un punto P’, situado sobre la recta SP definido por La imagen de P es P’ y la imagen de P’ es P. La inversión es una transformación recíproca.

1.4 CIRCULO DE INVERSION DE UNA INVERSION POSITIVA Una inversión positiva (p_i>0) tiene puntos dobles que están situados sobre un círculo de centro S y radio r= √p_i (sería P=P' y SP.SP'=SP²=p_i=r²). Una inversión negativa (p_i<0) no tiene puntos dobles (sería P=P' y SP.SP'=SP²<0).

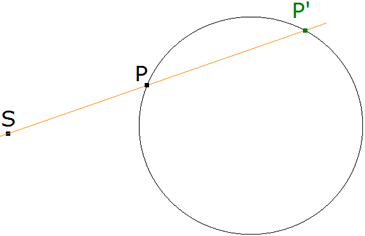
TEOREMA 1.5 (FIGURA INVERSA DE UNA RECTA) La inversa de una recta cualquiera es un círculo que pasa por el polo de inversión. Como transformación involutiva o recíproca, la figura inversa de un círculo que pasa por el polo de inversión es una recta.

DEMOSTRACION 1.5 figura 4 Por la propia definición, si la recta pasa por el polo de inversión, es inversa de ella misma. Sea una recta l, sea P’ el inverso de P (pie de la perpendicular desde el polo de inversión S a la recta l) y sea Q’ el inverso de Q (punto cualquiera de l), como SQ.SQ’=SP.SP’, entonces P, P’, Q, Q’ están en el mismo círculo (son cocíclicos) y por tanto SQ’ y P’Q’ forman un ángulo recto cuyos catetos pasan por sendos puntos fijos S y P’. Es claro que si variamos Q a lo largo de l, el lugar geométrico de Q’ es un círculo de diámetro SP’.

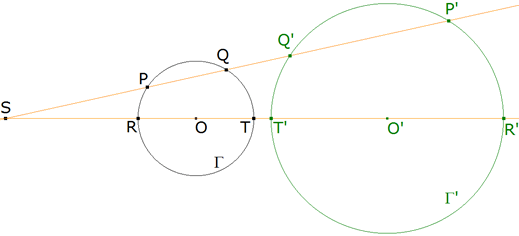
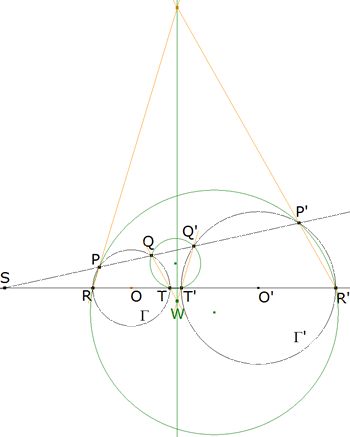
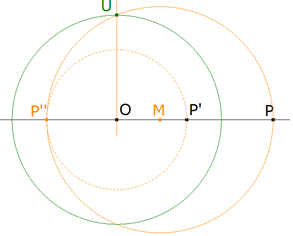
TEOREMA 1.6 (FIGURA INVERSA DE UN CIRCULO QUE NO PASA POR EL POLO) La figura inversa de un círculo que NO pasa por el polo de inversión, es un círculo.

figura 5 Primero cabe señalar que si la potencia de inversión (p_i) es igual a la potencia del polo de inversion S con respecto al círculo (p_c), la figura inversa del círculo es el mismo círculo. Una secante cualquiera desde S encuentra al círculo en dos puntos P y P’ que cumplen Si p_c es también la potencia de inversión, P’ es además el inverso de P y cuando P describe el círculo, P’ se desplaza sobre dicho círculo. 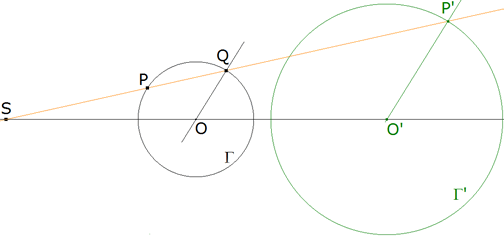Obviando este caso particular, consideremos un círculo Γ de centro O que no pasa por el polo de inversión S; tomamos un punto P del círculo cuyo inverso es P’. P’ está sobre SP y siendo p_i la potencia de inversión. DEMOSTRACION 1.6 figura 6 Buscamos el lugar geométrico del punto P’ cuando P se desplaza sobre el círculo Γ. La recta SP encuentra a Γ en un segundo punto Q y tenemos donde p_c designa la potencia del punto S respecto el círculo Γ. De las dos últimas ecuaciones pero eso significa que P’ es semejante a Q con centro de semejanza en S y razón p_i/p_c. Como el punto Q describe el círculo Γ, vemos que el lugar del punto P’ es el círculo Γ’, semejante a Γ según la semejanza indicada. Su centro O’ está sobre la recta SO y está definido por las relaciones Conviene observar que O’ ¡¡ NO !! es el inverso de O. La semejanza puesta de manifiesto nos dice que, si dos círculos son inversos, el polo de inversión sólo puede ser un centro de semejanza.

TEOREMA 1.7 (INTERCAMBIAR DOS CIRCULOS MEDIANTE UNA INVERSION) Dos círculos pueden ser considerados figuras inversas de dos modos distintos.

Sean Γ y Γ’ dos círculos de centros O, O’ y S su centro de semejanza exterior (demostración análoga podemos hacer con el centro de semejanza interior; pero la inversión sería negativa). Cualquier secante por S corta a Γ en P y Q y a Γ’ en Q’ y P’. Si en la semejanza de centro S, designamos a Q’ como el semejante de P y a P’ como el semejante de Q vamos a demostrar que P, P’ y Q, Q’ son pares de puntos inversos. Es decir aunque la secante varíe figura 7 DEMOSTRACION 1.7 Sea p_c la potencia del punto S respecto al círculo Γ, y sea k la razón de semejanza entre Γ’ y Γ. Se nos producen las igualdades siguientes dos círculos son figuras inversas, con polo de inversión S y potencia de inversión p_i=kp_c. Sea p’_c la potencia del punto S respecto al círculo Γ’, y sea 1/k la razón de semejanza entre Γ y Γ’. Se nos producen las igualdades siguientes COROLARIO 1.7 Para círculos tangentes, el punto de contacto es uno de los centros de semejanza (primera solución) y no puede ser centro de inversión ya que p_c=0 y por tanto p_i=kp_c=0. Para círculos iguales, un centro de semejanza va al infinito; no puede ser polo de inversión. En estos dos casos, sólo existe una única manera de considerar los círculos como inversos.

TEOREMA 1.8 Dos pares de puntos inversos, no situados sobre la misma secante, están en un círculo.

figura 8 DEMOSTRACION 1.8 Sean Q, Q’ y P, P’ los dos pares de puntos inversos en secantes diferentes. Cada uno de estos conjuntos de cuatro puntos están en el mismo círculo tal como hemos visto en 1.1

TEOREMA 1.9 Las cuerdas que unen dos puntos del círculo y las cuerdas que unen sus puntos inversos se cortan en el eje radical de los dos círculos.

figura 9 DEMOSTRACION 1.9 Sean W el punto de encuentro de dos cuerdas según el enunciado, QT, Q'T'; como los extremos de dichas cuerdas descansan sobre un círculo (TEOREMA 1.8) tenemos la igualdad muestra que W tiene la misma potencia respecto a Γ y a Γ’; luego W está sobre el eje radical.

2. LA INVERSION, CON REGLA Y COMPAS	solución 2

El programa CABRI II realiza las tares de inversión usando el círculo de inversión. Es pues importante saber como, conocidos dos puntos inversos y el centro de inversión, hallar el círculo de inversión. Para ello veremos primero como hallar el inverso de un punto dados el centro y el círculo de inversión y posteriormente veremos el recíproco.

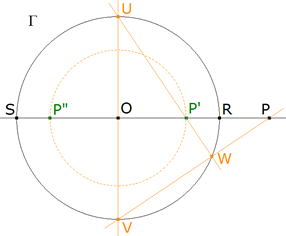
TEOREMA 2.1 Sea Γ el círculo de inversión de centro O y radio r y sea P’ el inverso de un punto P respecto a Γ; entonces P y P’ son los conjugados armónicos respecto el círculo Γ.

figura 10 DEMOSTRACION 2.1 Según 1.3, por ser P y P’ inversos respecto a Γ Pero ésta es además una de las definiciones de conjugación respecto a un círculo. Tomemos O como origen y OP como eje de abscisas; sea P la abscisa de P, p’ la abscisa de P’ y S y R de abscisas -r y r respectivamente. Si P y P’ son conjugados respecto a Γ, son conjugados armónicos de R y S; equivale a que la razón doble de los cuatro puntos es -1: y de aquí METODO 2.1 (INVERSION CON REGLA Y COMPAS) CONSTRUCCION DIRECTA: Dado un punto, el círculo y el centro, hallar el punto inverso figura 11 Observando la figura 11 y aplicando los visto en el párrafo anterior: a perpendicular a OP que corta a Γ en U y V b trazamos VP que corta a Γ en W c trazamos UW que corta a OP en P’ inverso de P d si la inversión es negativa el inverso es P”, simétrico de P’ respecto a O. Quien esté interesado puede comprobar que éste es una abreviación para el círculo de los distintos métodos de trazar polos y polares que aparecen en Gergonne y el Problema de Castillon de las páginas de RICARDO BARROSO CAMPOS. CONSRUCCION RECIPROCA: Dado un punto, el inverso y el centro, hallar el círculo figura 12 es la conocida construcción de la media geométrica OP.OP’=r² a P” simétrico de P’ respecto a O (cada lado de O). P” es inverso en el caso negativo. b M punto medio de P y P” como centro del círculo por P c perpendicular por O a OP que corta a este último círculo en U. d trazamos el círculo de centro O y radio OU.

3. IDENTIFICACION DEL PROBLEMA DE CASTILLON EQUIVALENTE	solución 2

Suponemos que el problema está resuelto y estudiamos la figura resultante (figura 14). Nos fijamos, por ejemplo, en el caso en el que los tipos de las tres tangencias coinciden (todas externas o todas internas); en este caso nos fijamos en el eje de semejanza externo.

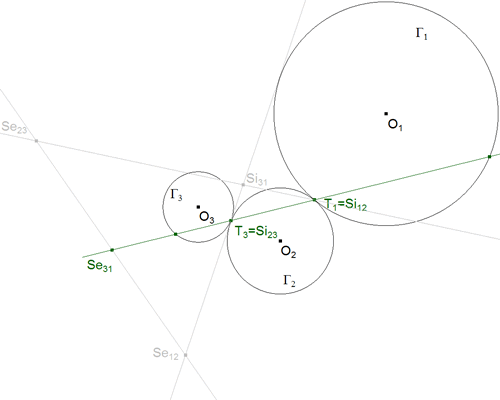
TEOREMA 3.1 (2.6 EN LA PRIMERA SOLUCION) Si un círculo Γ₂ es tangente en T₁ a un círculo Γ₁ y en T₃ a un círculo, Γ_3, la recta T₁T₃ pasa por uno de los centros de semejanza de los dos círculos Γ_1,Γ_3.

figura 13 DEMOSTRACION 3.1 Teniendo en cuenta los TEOREMAS 2.2 a 2.5 de la primera solución y en especial las configuraciones singulares en los casos de tangencia de los centros de semejanza (figuras 17 y 18 de la primera solución), el punto T₁ es Si₁₂, centro de semejanza interior de Γ₁ y Γ₂ el punto T₃ es Si₂₃, centro de semejanza interior de Γ₂ y Γ₃ Como hemos visto, en el TEOREMA 2.5 de la primera solución, estarán en la misma recta que el centro de semejanza exterior Se₃₁. NOTA 3.1 Si el círculo es tangente de la misma manera a los otros dos, es decir toca a los dos interiormente o toca a los dos exteriormente, la recta pasa por el centro de semejanza exterior; si por el contrario, es tangente de forma diferente, la recta pasa por el centro de semejanza interior.

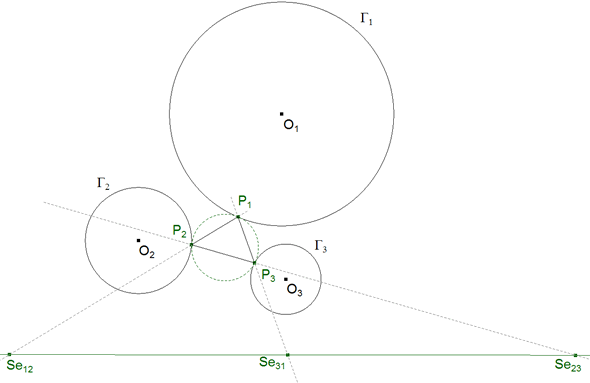
3.2 EL ENUNCIADO EQUIVALENTE PREVIO. Suponemos el problema resuelto y analicemos la figura. figura 14 ENUNCIADO ORIGINAL Trazar el círculo tangente a tres círculos dados Γ₁, Γ₂ y Γ₃. ENUNCIADO EQUIVALENTE PREVIO Hallar los puntos de contacto P₁, P₂ y P₃. Si construimos el eje de semejanza por Se₁₂, Se₂₃ y Se₃₁ y utilizamos el TEOREMA 3.1, P₁P₂pasa por Se₁₂, P₂ P₃ asa por Se₂₃, P₃P₁ pasa por Se₃₁.

3.3 EL PROBLEMA DE CASTILLON EQUIVALENTE AL PROBLEMA DE APOLONIO. Vemos que el problema que nos queda es el siguiente: “ Dado un círculo Γ (QUE NO CONOCEMOS) y tres puntos alineados Se₁₂, Se₃₁y Se₂₃; inscribir un triángulo en el círculo de forma que sus lados pasen por cada uno de los puntos dados. ” ES "CASI" EL PROBLEMA DE CASTILLON

4. UN PUNTO DE CONTACTO DESPUES DE TRES INTERCAMBIOS	solución 2

Sabemos por que puntos conocidos pasan las rectas que forman los puntos de contacto, es el PROBLEMA DE CASTILLON EQUIVALENTE; pero no conocemos los puntos de contacto y menos aún el círculo que definen (que es la solución). Si recordamos la resolución del Problema de Castillon por el método de PONCELET, búsqueda de puntos dobles de la homografía correspondiente, podemos salvar la situación; sólo hay que tener en cuenta la sugerencia de PETERSEN: ...SI TOMAMOS ESOS PUNTOS COMO CENTROS DE INVERSIÓN ELIGIENDO LAS POTENCIAS DE INVERSIÓN DE TAL MANERA QUE DOS CUALESQUIERA DE LOS CÍRCULOS SE INTERCAMBIAN ENTRE ELLOS, CADA UNO DE LOS CÍRCULOS DESPUÉS DE TRES INVERSIONES VOLVERÁ A LA POSICIÓN INICIAL.. Sigamos la sugerencia de PETERSEN y veamos el comportamiento de los puntos de contacto con esas tres inversiones.

Seguimos suponiendo el problema resuelto y recordemos que la recta que une dos puntos de contacto pasa por el centro de semejanza correspondiente (TEOREMA 3.1). figura 15 A partir del TEOREMA 1.6 que nos vincula semejanza e inversión deducimos siguiendo la figura 15 Intercambio Φe₁₂>:Γ₁→Γ₂ Como P₁ y P₂ están alineados con Se₁₂, la imagen de P₁ es P₂. Intercambio Φe₂₃:Γ₂→Γ₃ Como P₂ y P₃ están alineados con Se₂₃, la imagen de P₂ es P₃. Intercambio Φe₃₁:Γ₃→Γ₁ Como P₃ y P₁ están alineados con Se₃₁, la imagen de P₃ es P₁. En general, y para cada eje de semejanza existirá una función Φ que será composición de las Φe_jk y de las Φi_jk correspondientes Composición de los tres intercambios Φ:Γ₁→Γ₁ En el caso que estamos desarrollando ¡EL PUNTO DE CONTACTO DESPUÉS DE TRES INTERCAMBIOS PERMANECE FIJO!

5. UN PUNTO CUALQUIERA DESPUES DE TRES INTERCAMBIOS	solución 2

Después de ver, con el TEOREMA 3.1, el comportamiento de los puntos de contacto en los tres intercambios; pasamos a ver como se transforma un punto cualquiera por medio de los distintos círculo de inversión. Después de ver la equivalencia entre semejanza e inversión, bastaría trazar la recta desde el punto al centro de semejanza; pero entre recta y círculo hay dos intersecciones y en CABRI esas intersecciones no son estables (permutan). Por ello y para asegurar la estabilidad de la solución usaremos la inversión a través del círculo de inversión. En el caso de un problema estático, a mano, nos valdrían las simples intersecciones de recta y círculo. Señalado lo anterior intentamos determinar la naturaleza general de las transformaciones que intercambian círculos por inversión con polo en los centros de semejanza.

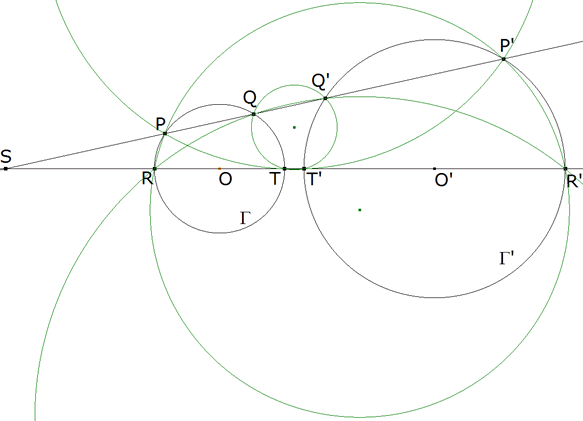
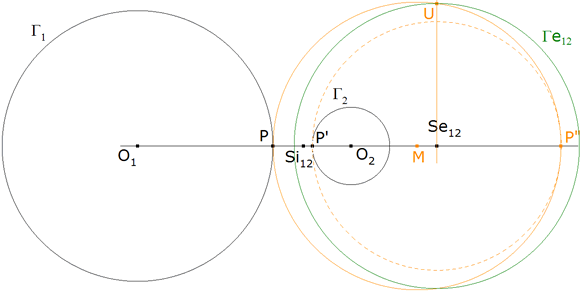
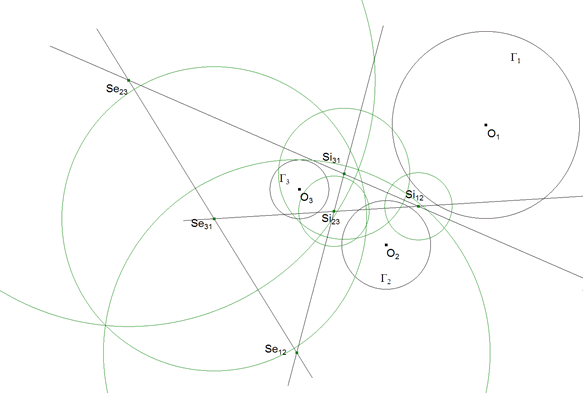
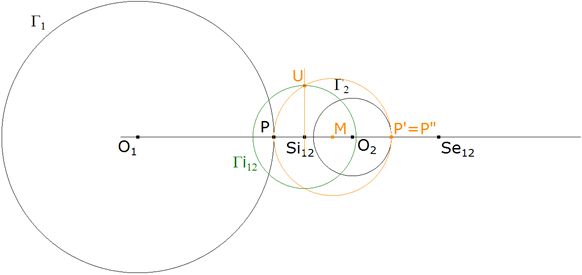
5.1 CIRCULO DE INVERSION QUE INTERCAMBIA DOS CIRCULOS PRIMER MODO DE INVERSIÓN: CENTRO EXTERIOR, INVERSIÓN POSITIVA figura 16 Usando la construcción recíproca del METODO 2.1 obtenemos Γe₁₂ que es el círculo de inversión que intercambia Γ₁ con Γ₂ por medio de una inversión positiva de polo Se₁₂. SEGUNDO MODO DE INVERSIÓN: CENTRO INTERIOR, INVERSIÓN NEGATIVA figura 17 Usando la construcción recíproca del METODO 2.1 obtenemos Γi₁₂ que es el círculo de inversión que intercambia Γ₁ con Γ₂ por medio de una inversión negativa de centro Si₁₂

LOS SEIS CIRCULOS QUE INTERCAMBIAN TRES CIRCULOS TOMADOS DOS A DOS igura 18

5.2 EL RECORRIDO DE UN PUNTO CUALQUIERA. P → Φ( P) (por ejemplo el eje Se₁₂Se₂₃Se₃₁) figura 19

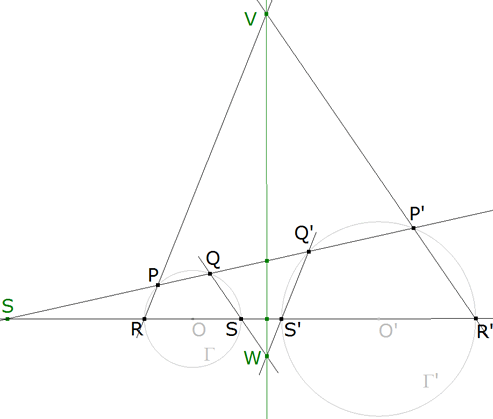
TEOREMA 5.3 (NATURALEZA DE LAS TRANSFORMACIONES Φ, Φe_kj, Φi_kj) La inversión Φe_kj (Φi_kj) que intercambia dos círculos Γ_j Γ_k es la restricción de una homología del plano con centro de homología el centro de semejanza de los dos círculos y con eje de homología el eje radical de los mismos.

figura 20 DEMOSTRACION 5.3 La identificación de la inversión mencionada con la semejanza (homotecia) nos da el camino de la demostración. Para el centro de homología vemos que: las rectas que unen un punto y su inverso pasan por un punto fijo del plano, el centro de semejanza S (TEOREMAS 1.6 Y 1.7). Para el eje de homología vemos que: Las rectas homólogas se encuentran sobre una recta (eje de homología); pero según el TEOREMA 1.9 esta recta es el eje radical de los dos círculos. NOTA 5.3 Recordemos que el punto semejante del centro de un círculo no se corresponde al inverso. ¡ LA RESTRICCION DE LA HOMOLOGIA SE LIMITA A LOS PUNTO SOBRE LA CIRCUNFERENCIA DE LOS CIRCULOS ! COROLARIO 5.3 La inversión que intercambia dos círculos Γ_j y Γ_k es la restricción de una homología del plano Φ_jk a los puntos de las circunferencias de dichos círculos. Φ_jk como homología del plano es una homografía, de lo que se deduce que para cada eje de semejanza, la función Φ, que para el eje Se₁₂Se₂₃Se₃₁ es es una homografía del plano; y como tal, la restricción a Γ₁ es una homografía del círculo sobre sí mismo (Ver el apartado 3 de Gergonne y el Problema de Castillon)

6. LA SOLUCION	solución 2

En este momento conocemos dos hechos fundamentales a Φ es una homografía de Γ₁sobre sí misma (TEOREMA 5.3) b los puntos de contacto P₁ son puntos fijos de la homografía (APARTADO 4) Hallamos el eje de la homografía (Ver TEOREMA 3.3 de Gergonne y el Problema de Castillon) y determinamos los puntos fijos. En general una recta (eje) corta a un círculo en dos puntos por lo que obtendremos un máximo de dos soluciones. Para ello tomaremos tres puntos cualesquiera de Γ₁ y buscaremos sus imágenes por Φ; es decir, veremos donde están después de las tres inversiones que señala PETERSEN. Con los dos puntos de contacto para cada uno de los cuatro eje de semejanza trazaremos en general las ocho soluciones.

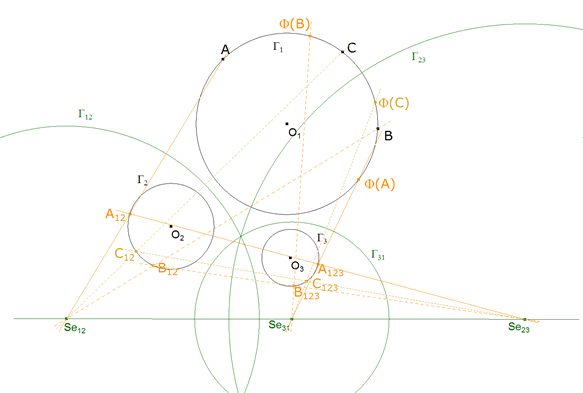
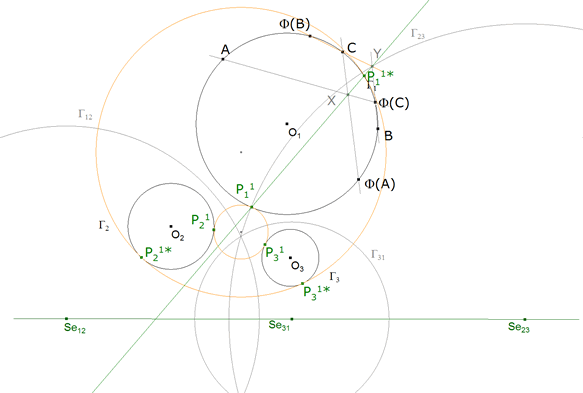
6.1 IMAGEN DE TRES PUNTOS CUALESQUIERA (Eje Se_12,Se_23,Se₃₁) figura 21 a Sea A sobre Γ₁ y hallamos Φe₁₂(A)=A₁₂ el inverso de A sobre Γ₂ (inversión CABRI) b Hallamos Φe₂₃(A₁₂)=A₁₂₃ el inverso de A₁₂ sobre Γ₃ c Hallamos Φe₃₁(A₁₂₃)=Φ(A) el inverso de A₁₂₃sobre Γ₁ d Repetimos lo anterior con B y C hasta hallar Φ(B) y Φ(C)

Aquí ya conocemos tres imágenes de la homografía Φ:Γ₁→ Γ₁. Podemos trazar su eje de homografía y obtener los puntos fijos, que son los puntos de contacto y por tanto el círculo tangente buscado.

6.2 EJE Se_12,Se_23,Se₃₁ Y PUNTOS DE CONTACTO (P₁¹, P₂¹, P₃¹) y (P₁¹, P₂¹, P₃¹). figura 22 e Recta por A y Φ(C), recta por C y Φ(A) se cortan en X f Recta por B y Φ(C), recta por C y Φ(B) se cortan en Y g XY eje de homografía que corta a Γ₁ en P₁¹ y en P₁¹, puntos fijos=puntos de contacto h Tomamos P₁¹ y hallamos P₂¹ el inverso de P₁¹ sobre Γ₂ (inversión CABRI II) i Tomamos P₂¹ y hallamos P₃¹ el inverso de P₂¹ sobre Γ₃ j Con los tres puntos de contacto P₁¹, P₂¹, P₃¹ trazamos el círculo tangente k Análogo para P₁¹* y hallamos el segundo círculo.

Para el resto de ejes de semejanza procedemos de igual modo teniendo especial atención con los centros de semejanza interiores que producen inversiones negativas y cuando eso ocurra, debemos efectuar además una simetría central. Hay que añadir orden y precaución cuando los puntos parecen confundirse unos con otros; por ello no nombraremos todos los puntos del dibujo con el fin de tener una figura clara.

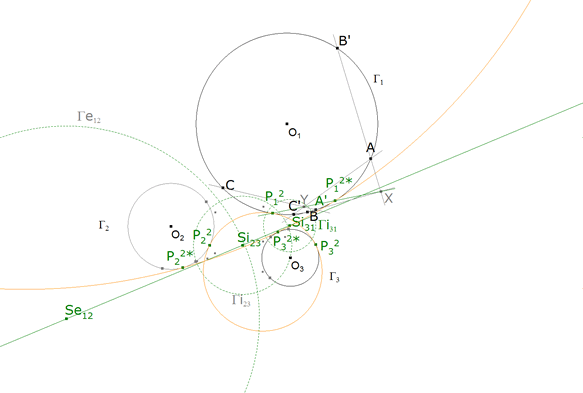
6.3 EJE Se_12,Si_23,Si₃₁ Y PUNTOS DE CONTACTO (P₁², P₂², P₃²) y (P₁², P₂², P₃²). figura 23 a Tomamos A en Γ₁, hallamos Φe₁₂(A)=A₁₂ el inverso de A en Γ₂ (inversión CABRI II) b Hallamos Φi₂₃(A₁₂)=A₁₂₃ el inverso y simétrico respecto Si₂₃ de A₁₂ en Γ₃ c Hallamos Φi₃₁(A₁₂₃)=Φ(A)=A’ el inverso y simétrico respecto Si₃₁ de A₁₂₃en Γ₁ d Repetimos lo anterior con B y C hasta hallar B’ y C’ e Recta por A y B’, recta por B y A’ se cortan en X f Recta por A y C’, recta por C y A’ se cortan en Y g XY eje de homografía que corta a Γ₁ en P₁² y en P₁², puntos fijos=puntos de contacto h Tomamos P₁² y hallamos P₂¹ el inverso de P₁¹ sobre Γ₂ i Tomamos P₁² y hallamos P₃² el inverso y simétrico respecto Si₃₁ de P₁² sobre Γ₃ j Con los tres puntos de contacto P₁², P₂², P₃² trazamos el círculo tangente k Análogo para P₁²* y hallamos el segundo círculo

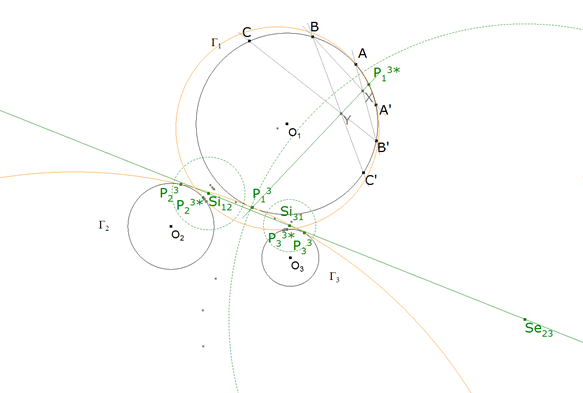
6.4 EJE Si_12,Se_23,Si₃₁ Y PUNTOS DE CONTACTO (P₁³, P₂³, P₃³) y (P₁³, P₂³, P₃³). figura 24 a Tomamos A en Γ₁, hallamos Φi₁₂(A)=A₁₂ el inverso y simétrico respecto Si₁₂ de A en Γ₂ b Hallamos Φe₂₃(A₁₂)=A₁₂₃ el inverso de A₁₂ en Γ₃ c Hallamos Φi₃₁(A₁₂₃)=Φ(A)= el inverso y simétrico respecto Si₃₁ de A₁₂₃en Γ₁ d Repetimos lo anterior con B y C hasta hallar B’ y C’ vigilando los centros interiores e Recta por A y B’, recta por B y A’ se cortan en X f Recta por B y C’, recta por C y B’ se cortan en Y g XY eje de homografía que corta a Γ₁ en P₁³ y en P₁³, puntos fijos=puntos de contacto h Tomamos P₁³ y hallamos P₂³ el inverso y simétrico respecto Si₁₂ de P₁³ sobre Γ₂ i Tomamos P₁³ y hallamos P₃³ el inverso y simétrico respecto Si₃₁ de P₁³ sobre Γ₃ j Con los tres puntos de contacto P₁³, P₂³, P₃³ trazamos el círculo tangente k Análogo para P₁³* y hallamos el segundo círculo

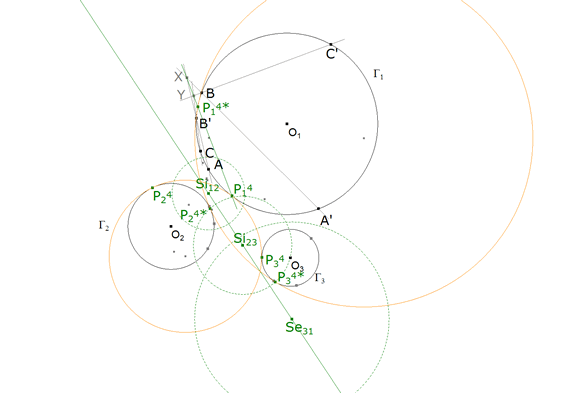
6.5 EJE Si_12,Si_23,Se₃₁ Y PUNTOS DE CONTACTO (P₁⁴, P₂⁴, P₃⁴) y (P₁⁴, P₂⁴, P₃⁴). figura 25 a Tomamos A en Γ₁, hallamos Φi₁₂(A)=A₁₂ el inverso y simétrico respecto Si₁₂ de A en Γ₂ b Hallamos Φi₂₃(A₁₂)=A₁₂₃ el inverso y simétrico respecto Si₂₃ de A₁₂ en Γ₃ c Hallamos Φe₃₁(A₁₂₃)=Φ(A)=A' el inverso de A₁₂₃en Γ₁ d Repetimos lo anterior con B y C hasta hallar B’ y C’ vigilando los centros interiores e Recta por A y B’, recta por B y A’ se cortan en X f Recta por B y C’, recta por C y B’ se cortan en Y g XY eje de homografía que corta a Γ₁ en P₁⁴ y en P₁⁴, puntos fijos=puntos de contacto h Tomamos P₁⁴ y hallamos P₂⁴ el inverso y simétrico respecto Si₁₂ de P₁⁴ sobre Γ₂ i Tomamos P₁⁴ y hallamos P₃⁴ el inverso de P₁⁴ sobre Γ₃ j Con los tres puntos de contacto P₁⁴, P₂⁴, P₃⁴ trazamos el círculo tangente k Análogo para P₁⁴* y hallamos el segundo círculo

LAS OCHO SOLUCIONES figura 26