1.23 ABC es un triángulo isósceles en el que A=120º.

Si BC es trisecado en D y E,

demostrar que ADE es un triángulo equilátero.

Aref, M.N. y Wernick, W. (1968): Problems & solutions in euclidean geometry.

Dover publications, Inc. New York. (p. 18)

Solución presentada por la Profa. Fabiola Czwienczek. Departamento de Matemática. UPEL – Maracay – Venezuela. al Problema 206

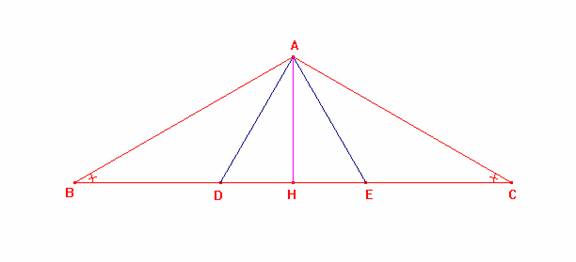
· Como el D ABC es isósceles con AB = AC y m (< BAC) = 120º, se deduce que

m (< B) = m (< C) = 30º

· Sea el segmento AH la altura del triángulo ABC correspondiente al vértice A. En consecuencia, el D AHC es un triángulo 30º - 60º - 90º, con m (< HAC) = 60º, m (< ACH) = 30º y m (< AHC) = 90º).

· Como el D AHC es un triángulo 30º - 60º - 90º, se tiene que 2AH = AC. (1)

· Sabemos que BD = DE = EC y que, además, AB = AC y m (< ABD) = m (< ACE). Por criterio LAL, D ABD @ D ACE. Por tanto, AD = AE y el D ADE es isósceles. De modo que, AH, como altura del D ADE, biseca a la base DE. Así 2HE = DE. Esto es, 2HE = EC. Nótese que HC = HE + EC = HE + 2HE = 3HE. (2)

· De (1) se establece que 4AH² = AC² = AH² + HC² (por el Teorema de Pitágoras). Así, pues, 3AH² = HC². (3)

· De (2), HC² = 9HE². (4)

· De (3) y (4): AH² = 3HE² (5)

· Trabajado en el D AHE, rectángulo: AE² = AH² + HE² = 3HE² + HE² = 4HE². Así, por ende, AE = 2HE.

· Por Teorema del triángulo 30º - 60º - 90º, m (< HAE) = 30º y, así, m (< AEH) = 60º. De manera que, m (< ADH) = 60º y, por ende, el D ADE es equilátero.

Solución presentada por la Profa. Fabiola Czwienczek. Departamento de Matemática. UPEL – Maracay – Venezuela.