Problema 206

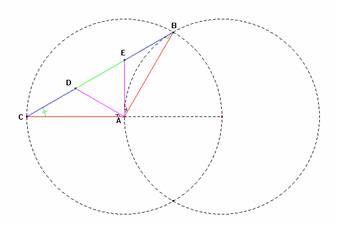
ABC es un triángulo isósceles en el que A=120º. Si BC es trisecado en D y E, demostrar que ADE es un triángulo equilátero.

Solución presentada por la Profa. Martha Iglesias Inojosa. Departamento de Matemática. UPEL – Maracay – Venezuela.

· El triángulo ABC es isósceles y obtusángulo con AB = AC y m (< A) = 120º. De modo que, m (< B) = m (< C) = 30º.

· El lado BC es trisecado en D y E, lo cual significa que CD = DE = EB = BC/3.

· De manera inmediata, por el criterio LLL, se establece que los triángulos ACD y ABE son congruentes y, en consecuencia que AD = AE. Por ende, el triángulo ADE es isósceles.

· Dado que el punto A equidista de los puntos D y E, se tiene que A pertenece a la mediatriz del segmento DE (en el plano determinado por los puntos A, B y C) y, por ende, los ángulos APD y APE son rectos, con D entre C y P y E entre B y P. Por ende, los triángulos ACP y ABP son triángulos 30º - 60º - 90º, con m (< PAC) = 60º y m (< PAB) = 60 º.

· Además, tal mediatriz AP biseca al ángulo DAE, de modo que:

m (< DAP) = m (< EAP) = a.

· Así, si m (< DAC) = b, se tiene que a + b = 60º.

· Como A equidista de B y C y P equidista de B y C, se cumple que la semirrecta AP también es la mediatriz de BC

· En el triángulo ACP, aplicando razones trigonométricas, se cumple que, si BC = X, entonces CP = X/2, AC = (Ö3/3)X y AP = (Ö3/6)X. Por otra parte, en el triángulo DAP, se tiene que DP = DE/2 = (BC/3)/2= X/6 y AD = X/3 (aplicando el teorema de Pitágoras).

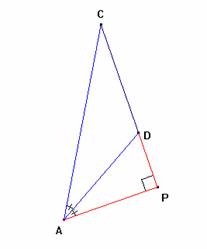
· De modo que, los triángulos ACP y DAP son semejantes y, por ende,

m (< C) = 30 º = m (< DAP) y m (< ADP) = m (< PAC) = 60º.

· Así, m (< AEP) = 60º = m (< ADP) y, por, ende el triángulo ADE es equiángulo y, por ende, equilátero.

· Obsérvese que pudieran establecerse otros resultados: los triángulos ACD y ABE son semejantes al triángulo original, según las siguientes correspondencias ACD « BCA y ABE « BCA; el segmento AD biseca al < PAC; el segmento AE biseca al < PAB; los triángulos ACE y ABD son también triángulos 30º - 60º - 90º. Lo interesante es poder establecer relaciones entre diversas definiciones y propiedades geométricas correspondientes a los programas de estudio a nivel de educación secundaria.

.