Problema 206
Para el aula
Problema 206
1.23 ABC es un triángulo isósceles en el que A=120º.
Si BC es trisecado en D y E,
demostrar que ADE es un triángulo equilátero.
Aref, M.N. y Wernick, W. (1968): Problems & solutions in euclidean geometry.
Solución de William Rodríguez Chamache. profesor de geometria de la "Academia integral class" Trujillo- Perú
Consideraciones iniciales:
Sabemos que si los segmentos MA=MB entonces la recta que contiene al segmento OM es bisectriz del ángulo O, por lo tanto los segmentos OA=OB (cuarto caso de congruencia LLA)
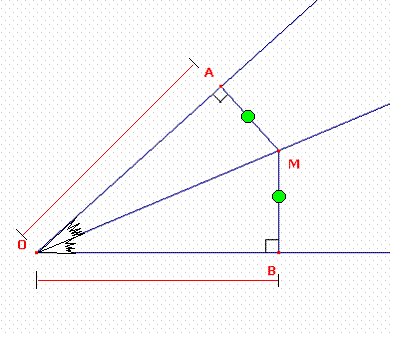
En la gráfica siguiente observaremos que los triángulos ABD y ACE son congruentes pro el caso (LAL)
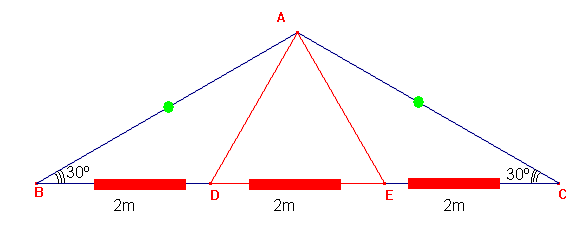
Ahora trazamos la perpendicular a los lados AB y AC que parten de los vértices D y E
Determinándose los triángulos rectángulos notable de 30 y 60 por lo tanto los segmentos ND=EN=m (mitad de la hipotenusa)
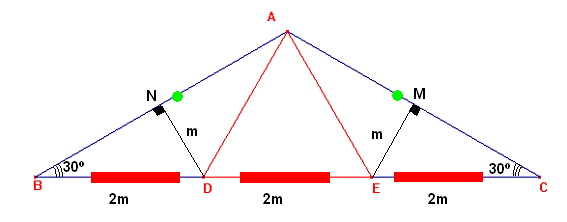
Ahora trazamos la altura del triángulo isósceles DAE que cae sobre la base determinado en está dos segmentos iguales DE=QE=m
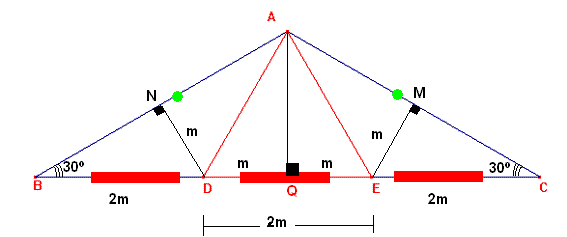
Finalmente de terminamos que los ángulos ÐNAD=ÐDAQ=ÐQAE=ÐAEC=α=30º
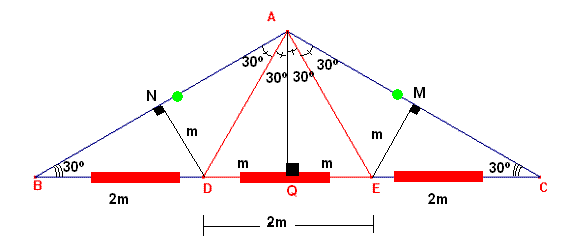
Por lo que se determina que el triángulo DAE es triángulo equilátero lqdqd
Prof. William Rodríguez chamache
Trujillo – Perú