És ben conegut que les bisectyrius d’un triangle divideixen el costat oposat en dos segments que són proporcionals als corresponents costats adjunts.

Generalitzant, considerarem el cas que els dos segments siguen proporcionals als quadrats dels costats adjunts.

Tal és el cas de la simediana, que és el simètric de la mitjana respecte de la bisectriu corresponent al mateix vèrtex.

Demostreu-ho, i una vegada demostrat, utilitzeu tal resultat a fi d’obtenir el punt de Lemoine, intersecció de les tres simedianes.

Yevdokimov, O. (2004) Skills of generalization in learning geometry. ARE THE STUDENTS READY TO USE THEM?

Solució de Peiró y Estruch, Ricard, profesor del IES 1 de Cheste :

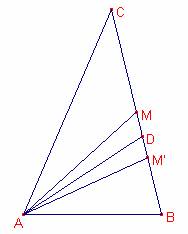
Siga el triangle

Siga  la mitjana.

Siga  la bisectriu.

Siga  segment simètric de  respecte de .

Siga .

Aplicant el teorema dels sinus al triangle :

 Aplicant el teorema dels sinus al triangle :

Dividint les expressions i aplicant el teorema dels sinus al triangle :

    (1)

Calculem les àrees dels triangles ,

Dividint les expressions:

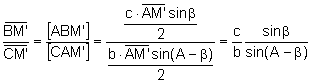     (2)

Substituint l’expressió (1) en l’expressió (2):

.

Aleshores, segments , són proporcionals als quadrats dels costats adjunts.

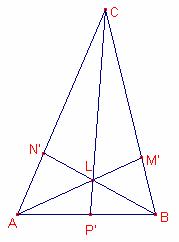Considerarem les tres simedianes .

Anàlogament provaríem que ,  .

Per a provar la segona part veurem que les tres simedianes acompleixen les hipòtesis del teorema de Ceva.

.

Aleshores les tres simedianes s’intersecten en un punt que s’anomena punt de Lemoine.