Problema 207

Es bien conocido que las bisectrices de un triángulo divide al lado opuesto en dos segmentos que son proporcionales a los correspondientes lados adjuntos.

Generalizando, consideremos el caso en que los dos segmentos sean proporcionales a los cuadrados de los lados adjuntos.

Tal es el caso de la simediana, que es el simétrico de la mediana resepcto a la bisectriz correspondiente al mismo vértice.

Demostrarlo, y una vez demostrado, utilizar tal resultado para obtener el punto de Lemoine, intersección de las tres simedianas.

Yevdokimov, O. (2004) Skills of generalization in learning geometry. ARE THE STUDENTS READY TO USE THEM?

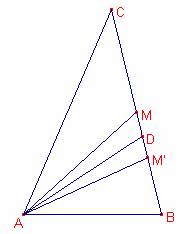SoluciónPeiró y Estruch, Ricard, profesor del IES 1 de Cheste:

Sea el triángulo

Sea  la mediana.

Sea  la bisectriz.

Sea  segmento simétrico de  respecto de .

Sea .

Aplicando el teorema de los senos al triángulo :

 Aplicando el teorema de los senos al triángulo :

Dividiendo las expresiones y aplicando el teorema de los senos al triángulo :

    (1)

Calculemos las áreas de los triángulos ,

Dividiendo las expresiones:

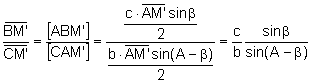     (2)

Substituyendo la expresión (1) en la expresión (2):

.

Entonces, segmentos , son proporcionales a los cuadrados de los lados adjuntos.

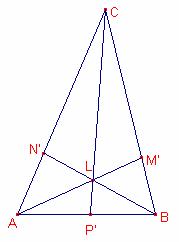Consideraremos las tres simedianas .

Análogamente probaríamos que ,  .

Para probar la segunda parte veremos que las tres simedianas cumplen las hipótesis del teorema de Ceva.

.

Entonces las tres simedianas se intersectan en un punto que se llama punto de Lemoine.