Problema 207

Es bien conocido que las bisectrices de un triángulo divide al lado opuesto en dos segmentos que son proporcionales a los correspondientes lados adjuntos.

Generalizando, consideremos el caso en que los dos segmentos sean proporcionales a los cuadrados de los lados adjuntos.

Tal es el caso de la simediana, que es el simétrico de la mediana resepcto a la bisectriz correspondiente al mismo vértice.

Demostrarlo, y una vez demostrado, utilizar tal resultado para obtener el punto de Lemoine, intersección de las tres simedianas.

Solución de Ricardo Linares Saldaña (Trujillo-Perú)

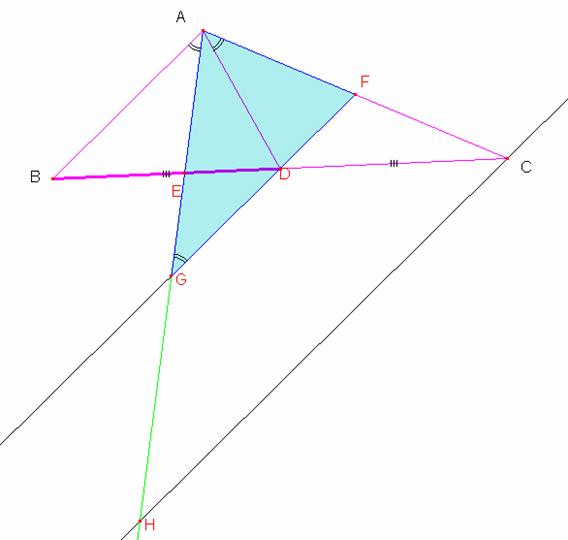
Se tiene el triangulo ABC, se traza la mediana AD y la simediana AE.

Se tiene que demostrar que

Se traza el rayo FG // AB // CH

En el triángulo AFG por semejanza se cumple que:

Entonces reemplazando: ………………………i

Pero , Lo mismo que: GD =ED.AB/BE ………………………ii

De i y ii:

AC²/4 = AB² ( 1/4 +.ED/2BE)

AC²/ AB² = (BE + 2ED)/BE , y EC = BE + 2ED

ENTONCES SE VERIFICA QUE: AC²/ AB² =EC/BE