Problema nº 207.- Es bien conocido que las
bisectrices de un triángulo divide al lado opuesto en dos segmentos que son
proporcionales a los correspondientes lados adjuntos.
Generalizando, consideremos el caso en que los dos
segmentos sean proporcionales a los cuadrados de los lados adjuntos.
Tal es el caso de la simediana, que es el simétrico de la
mediana respecto a la bisectriz correspondiente al mismo vértice.
Demostrarlo, y una vez demostrado, utilizar tal
resultado para obtener el punto de Lemoine, intersección de las tres simedianas.
Yevdokimov, O. (2004) Skills of generalization in learning geometry. ARE THE STUDENTS READY TO USE THEM?
Con permiso de su autor, Oleksiy Yevdokimov,
profesor de
Presentado al ICME 10 de Dinamarca.
Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León,
de Salamanca (8 de diciembre de 2004). -
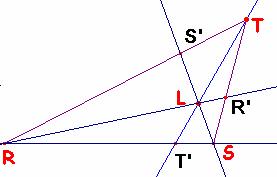
 Sea TP la bisectriz del ángulo RTS. Al tomar la recta simétrica de la mediana TT” respecto de la bisectriz, resulta que ésta es también
bisectriz del ángulo T” T T’. En
consecuencia, la mediana forma con el lado TR un
ángulo igual al que forma la simediana con el lado TS. Estas rectas son llamadas isogonales.
Sea TP la bisectriz del ángulo RTS. Al tomar la recta simétrica de la mediana TT” respecto de la bisectriz, resulta que ésta es también
bisectriz del ángulo T” T T’. En
consecuencia, la mediana forma con el lado TR un
ángulo igual al que forma la simediana con el lado TS. Estas rectas son llamadas isogonales.
Para demostrar la primera
parte utilizaremos:
- La razón de las áreas de dos triángulos con la misma altura es
igual a la razón de las bases respectivas.
- Área del triángulo RST: Área (RST) = ½ TR · TS · sen T.
Veamos en otra figura y con
carácter general qué relación hay entre los segmentos determinados sobre el
lado opuesto por dos isogonales.
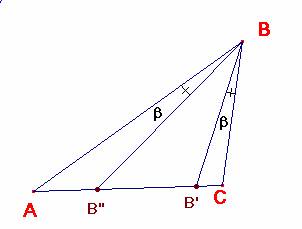 Comparando las áreas de los triángulos
CB”B y B’AB por una parte
y las de los triángulos B”AB y CB’B por otra, tenemos:
Comparando las áreas de los triángulos
CB”B y B’AB por una parte
y las de los triángulos B”AB y CB’B por otra, tenemos:
![]()
![]()
Dividiéndolas entre sí :
![]() .
.
En el caso particular en que B” sea el punto
medio de AC ésta última relación se simplifica pues B”A = CB”
quedando ![]() . Para el triángulo
RST la relación es
. Para el triángulo
RST la relación es ![]() que es lo que
pretendíamos demostrar.
que es lo que
pretendíamos demostrar.
Para las otras dos simedianas se tienen las relaciones ![]() y
y ![]() .
.
La concurrencia de las tres
simedianas en el punto de Lemoine L,
se obtiene de inmediato sin más que
aplicar el teorema de Ceva al triángulo en el que se han calculado previamente
las tres rectas simedianas: el producto
de las tres razones anteriores vale 1. c.q.d.