Problema 207
Es bien conocido que las bisectrices de un triángulo dividen al lado opuesto en dos segmentos que son proporcionales a los correspondientes lados adjuntos.
Generalizando, consideremos el caso en que los dos segmentos sean proporcionales a los cuadrados de los lados adjuntos.
Tal es el caso de la Simediana, que es el simétrico de la mediana respecto a la bisectriz correspondiente al mismo vértice.
Demostrarlo, y una vez demostrado, utilizar tal resultado para obtener el punto de Lemoine, intersección de las tres simedianas.
Yevdokimov, O. (2004) Skills of generalization in
learning geometry.
ARE THE STUDENTS READY TO USE THEM?
Con permiso
de su autor, OleksiyYevdokimov, profesor de la
Presentado al ICME 10 de Dinamarca.
SOLUCIÓN de la segunda parte de William Rodríguez Chamache. profesor de geometria de la "Academia integral class" Trujillo- Perú (10 de diciembre de 2004)
Por propiedad sabemos que si tres cevianas se interceptan en un punto entonces el producto de los segmento no consecutivos determinados en cada uno de sus lados es igual al producto de los otros tres.
Del gráfico se cumple que: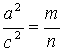 
Del gráfico se cumple que: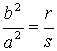 
Del grafico. Se cumple que: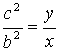 
Multiplicando las tres ecuaciones:
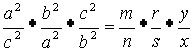
Finalmente obtenemos: que: 
por lo tanto las
simedianas se interceptan en el punto W denominado punto de Lemoine
