Problema 208. Un triángulo
equilátero inscrito.
"Dado un triángulo, mostrar cómo se construyen tres puntos, uno en cada lado, de manera que formen los vértices de un triángulo equilátero."
Bryant,
V.W. y Austin, A.K. (1983): Reading in Mathematical Education. Geometry. Seleccionado por Marion Walter. Association of Teachers of
Mathematics. Los profesores Bryant y Austin estaban en la
Universidad de Scheffield. Traducción de Ricardo
Barroso Campos.(Didáctica de las Matemáticas) Universidad de Sevilla.
Solución.-
a) Supongamos el problema resuelto,
si elegimos un vértice del triángulo equilátero, por ejemplo el B’, un giro con centro en él y amplitud 60º lleva la
recta a=BC a la recta a’ y el vértice A’ al vértice C’ sobre la recta AB (y también
sobre a’ ).
Por tanto, para realizar la construcción se elige un
punto cualquiera B’ sobre AC y se sigue el procedimiento explicado antes para
hallar C’. Un segundo giro de 60º y centro C’ transforma b=AC en b’ y el vértice B’ en
el A’ quedando completamente determinado
el triángulo.

b) Si en vez de intentar inscribir un triángulo equilátero cualquiera, queremos que sus lados sean paralelos a los de otro triángulo equilátero dado, la cuestión se complica, ya no hay infinitas soluciones como antes.
Recurrimos primeramente a los procedimientos de la geometría proyectiva.
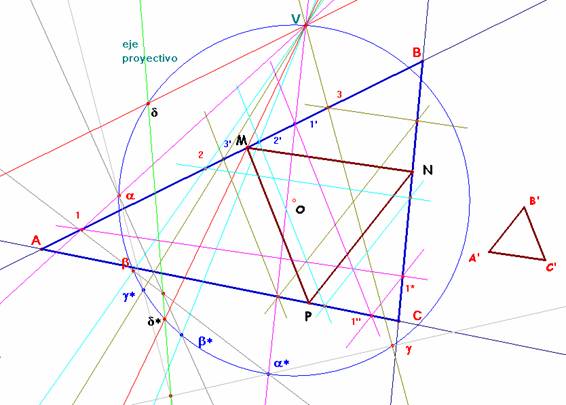
Tomando un punto 1 en el lado AB, lo proyectamos en 1* sobre el lado BC según la dirección paralela al lado A’C’ del triángulo equilátero dado; de aquí y paralelo a A’B’ se proyecta en 1” sobre AC y, finalmente, según B’C’ se proyecta en 1’ otra vez sobre AB.
El recorrido, en AB, desde el punto 1 hasta el punto 1’ se ha realizado a través de proyecciones y por eso se trata de una proyectividad sobre esta recta. Si en este recorrido, el punto origen y el punto final fueran iguales, habríamos dado con la solución buscada. Al proceder por tanteo esto no sucede así.
Los puntos dobles ─si los hay─ de la proyectividad definida por esta sucesión de proyecciones son las soluciones del problema.
Para hallarlos necesitamos las imágenes de tres puntos 1, 2 y 3.
La proyectividad sobre AB queda definida por
(1, 2, 3 ) à(1’, 2’, 3’).
Proyectamos estos puntos y sus homólogos desde un punto
exterior cualquiera V.
Tenemos una proyectividad entre dos haces de rectas definida por
(V1, V2, V3 ) à (V1’, V2’, V3’ )
y estos haces los cortamos con una circunferencia cualquiera de centro O que pase por el vértice V (en lugar de la circunferencia puede ponerse cualquier cónica que pase por V). Se determina el eje proyectivo de esta nueva proyectividad sobre la circunferencia ─la definida por (a, b, g )à( a*, b*, g*) ─ el cual corta a la circunferencia en los puntos dobles d, d*. La proyección desde V sobre la recta AB nos da los puntos dobles buscados. Observamos que sólo hay uno (las rectas Vd y AB son paralelas, con lo cual el otro punto doble está en el infinito), lo que indica la existencia de una única solución afín[1].
El método para hallar los puntos dobles es el mismo que
se utilizó en el problema nº 82 (Problema de Castillon) y en el problema nº
137
c) También puede hacerse la construcción de esta otra forma:
Por los vértices del triángulo ABC se trazan paralelas a los lados del triángulo MNP. Se construye así el triángulo equilátero de lados paralelos M’N’P’. Otra vez por los vértices de éste trazamos paralelas a los lados de ABC. Formamos A’B’C’ y uniendo vértices homólogos en la semejanza fijamos H, su centro.
El triángulo deseado M*N*P* es homotético a M’N’P’ ; el centro de homotecia es también H, y su trazado resulta inmediato. (M* y M’ son homólogos en la homotecia que transforma BC en B’C’ e igual los demás vértices).
