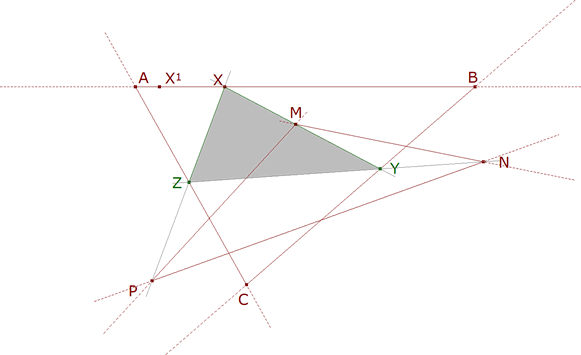
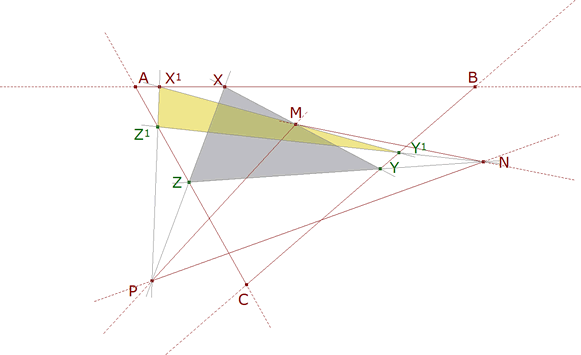
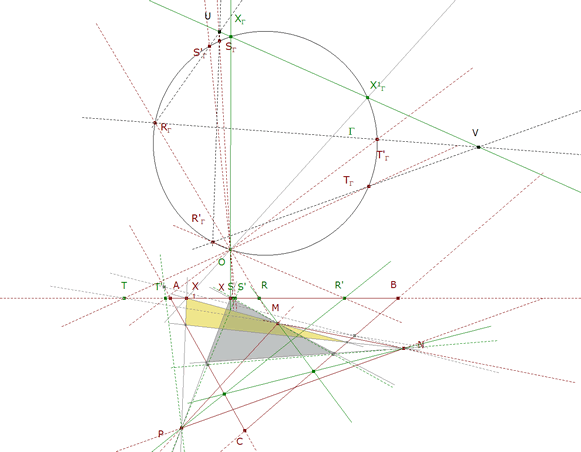
Dado un triángulo ABC y un triángulo MNP, hallar el triángulo XYZ cuyos vértices se apoyen en los lados de ABC y cuyos lados pasen por los vértices de MNP
Primera solución José María Pedret. Ingeniero Naval. Esplugues de Llobregat (Barcelona). 16 de enero de 2005 |
|
0. INTRODUCCION |
|
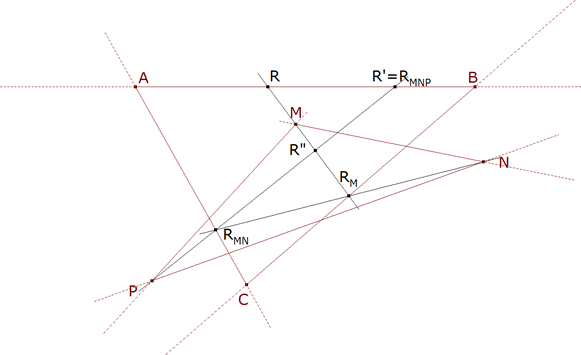
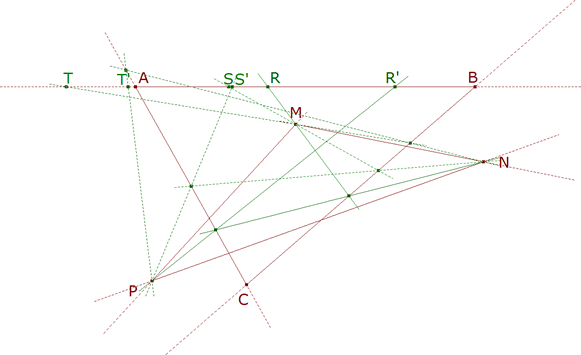
Suponemos que R, un punto cualquiera sobre el lado AB del primer triángulo, es el vértice sobre AB. El lado por este vértice R ha de pasar por M, uno de los vértices del segundo triángulo; la recta MR corta al lado BC en RM. Si RM es el vértice sobre BC, el lado por RM ha de pasar por N, segundo vértice del segundo triángulo; NRM corta a CA en RMN. El lado por RMN ha de pasar por P y PRMN corta al lado AB en RMNP.
RMNP=R’=R=R”
Si somos capaces de determinar la relación que existe entre R y R’ estableceremos la condición para que R y R’ coincidan. |
|
1. ¿QUÉ TRANSFORMACIÓN CONVIERTE A R EN RM? |
|
HOMOGRAFÍAS Sólo consideraremos que son biyecciones entre espacios proyectivos que conservan la razón doble de cuatro puntos. Recordemos algunas propiedades:
a) La composición de homografías es una homografía.
b) La homografía transforma puntos alineados en puntos alineados. De ello se deduce que una homografía entre espacios proyectivos P y P’ transforma toda recta de P en una recta de P’. La transformación a estudiar toma un punto de una recta y lo transforma en un punto de otra recta y como que a cada punto de AB le corresponde un único punto de BC, la transformación es claramente una biyección. Veamos si es una homografía. |
|
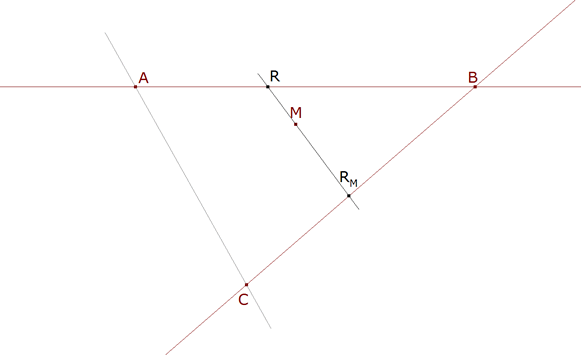
LAS PROYECCIONES Sean AB ,BC dos rectas proyectivas de un plano proyectivo y M un punto de ese plano que no pertenece ni a AB ni a BC. La aplicación de AB sobre BC que a un punto R de AB asocia un punto R’
πM:AB→BC;
πM(R)=RM∩BC=RM, R∈AB
recibe el nombre de proyección central de centro M de AB sobre BC.
(r1,r2,r3,r4)=(P1,P2,P3,P4). Así,la proyección entre rectas proyectivas es una biyección que conserva la razón doble y por tanto es una homografía. Se puede demostrar que una homografía entre dos rectas distintas de un plano proyectivo es una proyección si y sólo si el punto de intersección de estas rectas se transforma en sí mismo.
πN:BC→CA; πN(RM)=NRM∩CA=RMN, RM∈BC πP:CA→AB; πP(RMN)=PRMN∩AB=RMNP, RMN∈CA |
|
2. ¿QUÉ TRANSFORMACIÓN CONVIERTE A R EN R’? |
|
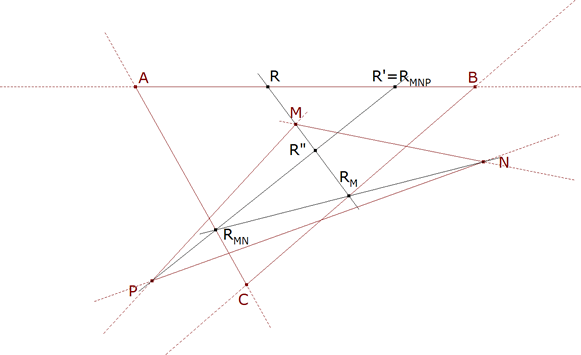
A nosotros nos interesa, para hallar la solución, que se cumpla la igualdad entre el punto inicial y el punto final
RMNP=R’=R
πP(πN(RM))=R πP(πN(πM(R)))=R
πP◦πN◦πM(R)=R.
Una proyección entre rectas proyectivas es una homografía y la composición de homografías es homografía.
hr:AB→AB con R’=hr(R)=πP◦πN◦πM(RM)
y la solución X cumplirá
hr(X)=πP◦πN◦πM(X) |
|
3. PUNTOS FIJOS DE UNA HOMOGRAFIA DE LA RECTA PROYECTIVA |
|
El método más directo para hallar gráficamente los puntos fijos de una homografía de la recta proyectiva sobre sí misma pasa por saber determinar los puntos fijos de una homografía de una cónica sobre sí misma. En Gergonne y el problema de Castillon (problema 200a), ya vimos como hallar los puntos fijos (puntos dobles) de una homografía de la cónica sobre sí misma. Sólo debemos saber vincular las homografías de la recta sobre sí misma con las homografías de la cónica sobre sí misma. La respuesta, de nuevo, está en las proyecciones. |
|
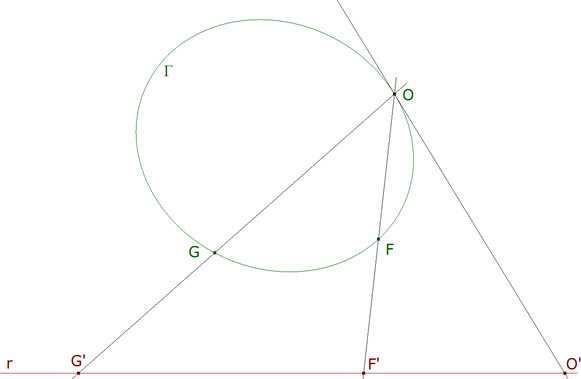
3.1 PROYECCIÓN DE UNA CONICA SOBRE UNA RECTA
Sea O un punto de una cónica Γ y r una recta que no pasa por O. Sea F un punto de Γ; la recta OF corta a r en F’ (si F está en O, la recta OF es naturalmente la tangente a Γ en O y corta a r en O’). Se obtiene así una biyección
π:Γ→r,
Como hemos visto al inicio, queda claro que esta biyección deja invariante la razón doble de cuatro puntos. Esta biyección recibe el nombre de proyección de la cónica Γ sobre la recta r desde un punto O. Podemos decir además que esta proyección es una homografía de Γ sobre r.
π-1:r→Γ,
Consideremos ahora una homografía
α:Γ→Γ
de la cónica Γ sobre sí misma. La aplicación
π◦α◦π-1:r→r define una homografía de r sobre sí misma. Recíprocamente, si
α’:r→r es una homografía de la recta r sobre sí misma, la biyección
π-1◦α’◦π:Γ→Γ es una homografía de la cónica Γ sobre sí misma. Es inmediato que la aplicación
ψ:G(Γ)→G(r) con ψ(α)=π◦α◦π-1 define un isomorfismo del grupo G(Γ) de las homografías de Γ sobre el grupo G(r) de las homografías de r.
α→π◦α◦π-1, donde π es la proyección de la cónica Γ sobre la recta r desde el punto O, define un isomorfismo entre el grupo de homografías de Γ y el grupo de homografías de r. Se define de igual manera la proyección de Γ sobre el haz O*, siendo O un punto elegido sobre Γ. Esto permite definir también un isomorfismo entre el grupo de homografías de Γ y el grupo de homografías de O*. LO VISTO EN ESTE APARTADO PERMITE APLICAR A LAS HOMOGRAFÍAS DE LA CONICA LOS RESULTADOS GENERALES DE LAS HOMOGRAFÍAS DE LA RECTA. |
3.2 DETERMINACION DE LOS PUNTOS FIJOS DE LA HOMOGRAFIA DE LA RECTA
gΓ=π◦hr◦π-1
es una homografía de la cónica sobre sí misma. Sus puntos fijos XΓ cumplen
gΓ(XΓ)=XΓ π◦gΓ(XΓ)=π(XΓ) π◦gΓ(π-1(X))=π(π-1(X)) π◦gΓ◦π-1(X)=X=h(X)
por lo tanto: LAS IMÁGENES POR LA PROYECCIÓN DE LOS PUNTOS DOBLES DE LA HOMOGRAFÍA DE LA CÓNICA SOBRE SÍ MISMA SON LOS PUNTOS DOBLES DE LA HOMOGRAFÍA DE LA RECTA SOBRE SÍ MISMA. |
4. SOLUCION |
|
Para determinar la homografía hr de la recta AB sobre sí misma hallaremos la imagen de tres puntos. Luego proyectaremos la recta sobre una cónica. Escogeremos un círculo porque es más simple y un punto O que nos proporcione la proyección más clara posible. Lo anterior define una homografía del círculo sobre sí mismo. Hallamos sus puntos dobles (dos intersecciones como máximo con su eje de la homografía). Con el inverso de la proyección determinamos los puntos dobles en la recta. Con los puntos dobles en AB hallamos los triángulos solución de nuestro enunciado original. |
|
4.1 LA SOLUCION PASO A PASO
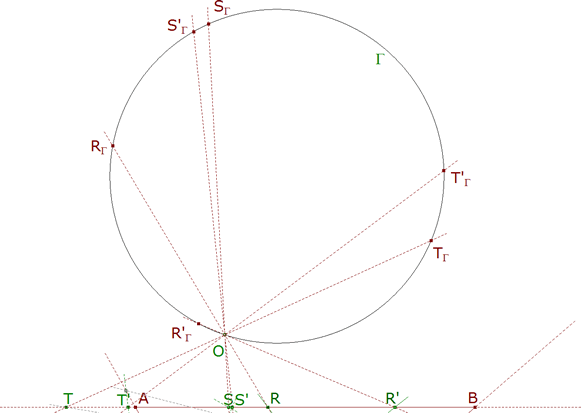
a) Del mismo modo que de hemos obtenido hr(R)=R’, obtenemos hr(S)=S’y hr(T)=T’
b) Trazamos ahora un círculo Γ cualquiera y elegimos sobre él un punto O de forma conveniente.
Proyectamos la recta AB sobre el círculo Γ. Por ejemplo
π-1(R)=OR∩Γ=XΓ
Queda así definida la homografía del círculo sobre sí mismo.
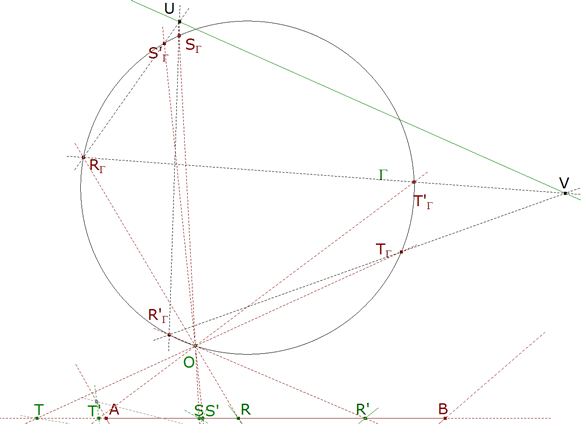
c) Hallamos UV, eje de la homografía del círculo sobre sí mismo.
U=RΓS'Γ∩SΓR'Γ
V=RΓT'Γ∩TΓR'Γ
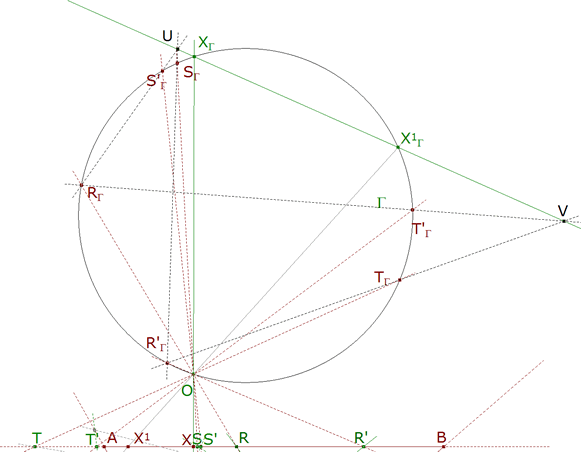
d) Hallamos los puntos doble XΓ y X1Γ de la homografía del círculo sobre sí mismo
{XΓ,X1Γ}=UV∩Γ
Proyectamos ahora estos puntos sobre la recta
X=OXΓ∩AB
X1=OX1Γ∩AB
e) MX corta a BC en Y, PX corta a CA en Z. Trazamos el triángulo XYZ.
f) MX1 corta a BC en Y1, PX1 corta a CA en Z1. Trazamos el triángulo X1Y1Z1. |
4.2 TODO JUNTO
|