Dado un triángulo ABC y un triángulo MNP, hallar el triángulo XYZ cuyos vértices se apoyen en los lados de ABC y cuyos lado pasen por los vértices de MNP Segunda solución José María Pedret. Ingeniero Naval. Esplugues de Llobregat (Barcelona). 16 de enero de 2005

0. INTRODUCCION	Segunda solución

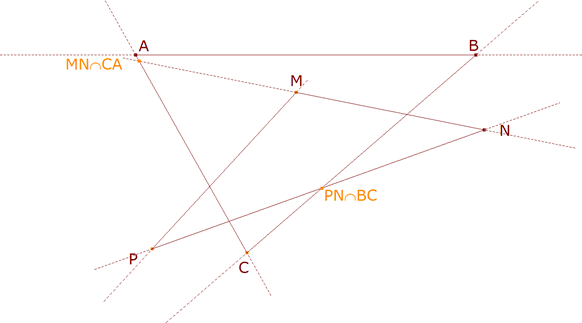
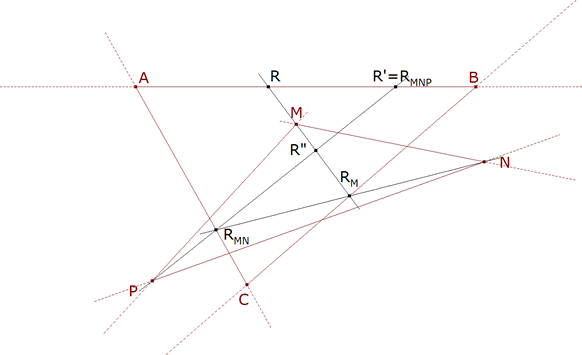
Empezamos igual que en la primera solución. figura 1 Supongamos que R, un punto cualquiera sobre el lado AB del primer triángulo, es el vértice sobre AB. El lado por este vértice R ha de pasar por M, uno de los vértices del segundo triángulo; la recta MR corta al lado BC en R_M. Si R_M es el vértice sobre BC el lado por R_M ha de pasar por N, segundo vértice del segundo triángulo; la recta NR_M corta al lado CA en el punto R_MN. El lado por R_MN ha de pasar por P y la recta PR_MN corta a AB en R_MNP. 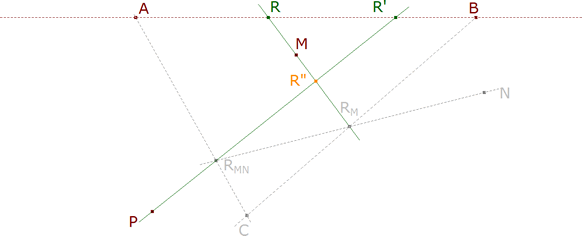R_MNP y R en general no coinciden, si R_MNP coincidiese con R habríamos conseguido la solución, y sería R_MNP = R’ = R = R” A partir de aquí, tomamos una ruta completamente distinta a la de la primera solución. Si somos capaces de determinar el lugar geométrico que describe R” = MR∩PR’. Cuando R” esté sobre AB, coincidirá con R y R’ y habremos obtenido las soluciones si existen. Vamos a ver que el lugar geométrico existe y es una CÓNICA. Las intersecciones, si las hay, de esta cónica con la recta AB nos da las posibles soluciones. Esta intersección se resuelve con regla y compás; y en el estudio del problema 137, si sólo tenemos los cinco puntos que definen una cónica, se explica como hacerlo.

1. ¿QUÉ TRANSFORMACIÓN CONVIERTE A R EN R_m?	Segunda solución

HOMOGRAFÍAS Sólo consideraremos que son biyecciones entre espacios proyectivos que conservan la razón doble de cuatro puntos. Recordemos algunas propiedades: a) la composición de homografías es una homografía b) una homografía transforma puntos alineados en puntos alineados. En consecuencia, una homografía entre espacios proyectivos P y P’ transforma toda recta de P en una recta de P’. La transformación a estudiar toma un punto de una recta y lo transforma en un punto de otra recta y como que a cada punto de AB le corresponde un único punto de BC, la transformación es claramente una biyección. Veamos si es una homografía.

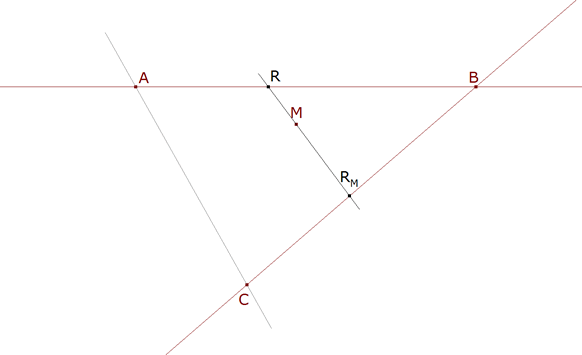
figura 2 LAS PROYECCIONES Sean AB, BC dos rectas proyectivas de un plano proyectivo y M un punto de ese plano que no pertenece ni a AB ni a BC. La aplicación de AB sobre BC que a un punto R de AB asocia un punto R’ de BC π_M:AB→BC π_M(R) = MR∩BC = R_M, R∈AB recibe el nombre de proyección central de centro M de AB sobre BC. Recordamos que en el plano proyectivo, cuatro rectas distintas r₁, r₂, r₃, r₄, que pasan por un punto fijo O y son cortadas por una secante s, que no pasa por O, en los puntos P₁, P₂, P₃, P₄, cumplen que la razón doble de las rectas es igual a la razón doble de los puntos (r₁,r₂,r₃,r₄) = (P₁,P₂,P₃,P₄) Es claro entonces que la proyección entre rectas proyectivas es una biyección que conserva la razón doble y por tanto es una homografía. Se puede demostrar que una homografía entre dos rectas distintas de un plano proyectivo es una proyección si y sólo si el punto de intersección de estas rectas se transforma en sí mismo. De forma análoga observamos dos proyecciones más (ver figura 1) π_N:BC→CA, π_N(R_M) = NR_M∩CA = R_MN, R_M∈BC π_P:CA→AB π_P(R_MN) = PR_MN∩AB = R_MNP, R_MN∈CA

2. ¿QUÉ TRANSFORMACIÓN CONVIERTE A R EN R’?	Segunda solución

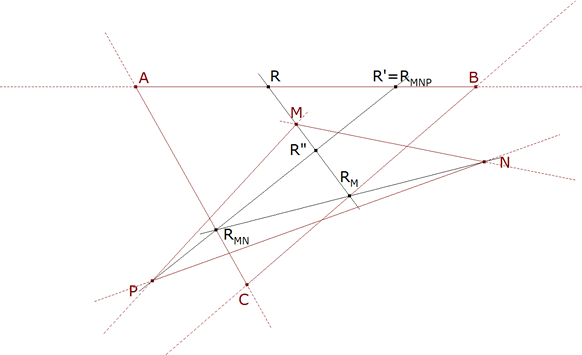
figura 3 R’ = R_MNP R’ = π_P(R_MN) R’ = π_P(π_N(R_M)) R’ = π_P(π_N(π_M(R))) R’ = π_P◦π_N◦π_M(R) Por lo tanto la transformación que transforma al punto R en R’ es la composición de tres proyecciones entre los lados del triángulo ABC con centros de proyección respectivos en los vértices del triángulo MNP. Una proyección entre rectas proyectivas es una homografía y la composición de homografías es homografía. LA TRANSFORMACIÓN BUSCADA ES UNA HOMOGRAFÍA DEL LADO AB DEL PRIMER TRIÁNGULO ABC SOBRE SÍ MISMO Y EL PUNTO SOLUCIÓN UN PUNTO FIJO DE ESTA HOMOGRAFÍA. h_AB:AB→AB con R’ = h_AB(R) = R’ = π_P◦π_N◦π_M(R)

3. HOMOGRAFIA ENTRE LOS HACES M* y P*	Segunda solución

Establecemos en este apartado una homografía entre el haz de todas las rectas que pasan por M, y el haz de todas las rectas que pasan por P. Y lo hacemos de la siguiente manera DATOS Sea una recta AB. Sea una homografía de la recta AB sobre sí misma h_r:AB→AB con h_r(R)= R’. Sean dos puntos fijos M, P y los haces de rectas por ellos M, P. DEFINICIONES h_AB:AB→AB (definida en el APARTADO 2) φ_M:AB→M* con φ_M(R) = MR φ_P:AB→P* con φ_P(R’) = PR’ h_AB:M→P* con h*_AB(MR) = PR’ NOTA PARA QUIEN QUIERA CORRER En este apartado ya podríamos caracterizar el lugar geométrico de R” pues una manera de enunciar el TEOREMA DE CHASLES-STEINER es la siguiente: En un plano proyectivo sea h_AB:AB→AB una biyección de la recta AB; para todo par de puntos distintos M, P no situados sobre AB, el punto MR∩Ph_AB(R) es de una cónica que pasa por M y P, si y sólo si h_AB es una homografía. ¡NOSOTROS IREMOS MAS DESPACIO!

3.1 h_AB ES UNA HOMOGRAFÍA figura 4 φ_M:AB→M con φ_M(R) = MR es una homografía. Por su definición que es una biyección. Recordando, de nuevo, que en el plano proyectivo, cuatro rectas distintas r₁, r₂, r₃, r₄ que pasan por un punto fijo O y son cortadas por una secante s, que no pasa por O, en los puntos P₁, P₂, P₃, P₄ cumplen que la razón doble de las rectas es igual a la razón doble de los puntos; que en nuestro caso, tomando AB como secante, (R₁,R₂,R₃,R₄) = (MR₁,MR₂,MR₃,MR₄) = (φ_M(R₁),φ_M(R₂),φ_M(R₃),φ_M(R₄)) y queda claro que esta biyección deja invariante la razón doble de cuatro puntos y por lo tanto es una homografía. φ_P:AB→P* con φ_P(R’)= PR’ es una homografía. Mismo procedimiento que en el caso anterior. h_AB:M→P* con h_AB(MR)= PR’es una homografía. h_AB(MR) = PR’ = φ_P(R’) h_AB(MR) = φ_P(R’) = φ_P(h_AB(R)) h_AB(MR) = φ_P(h_AB(R)) = φ_P(h_AB(φ_M^-1(MR))) h_AB = φ_P◦h_AB◦φ_M^-1 h_AB ES UNA COMPOSICIÓN DE HOMOGRAFÍAS Y POR LO TANTO ELLA MISMA ES UNA HOMOGRAFÍA.

4. EL LUGAR GEOMETRICO DE R”	Segunda solución

4.1 TEOREMA DE CHASLES STEINER El lugar geométrico del punto de intersección de las rectas que se corresponden en una homografía entre haces de rectas es una cónica. Y recíprocamente. Recordemos que si una de las rectas se corresponde a sí misma, la homografía es una proyección entre haces de rectas y el lugar geométrico es una recta. Si los haces son M* y P* la cónica pasa por M y P. La imagen de la recta MP es la tangente en P a la cónica y la anti-imagen de PM es la tangente en M a la cónica. Se puede ver la demostración en la Universidad de Michigan Michel Chasles, Traité des sections coniques Más sobre el tema en la solución del problema 182

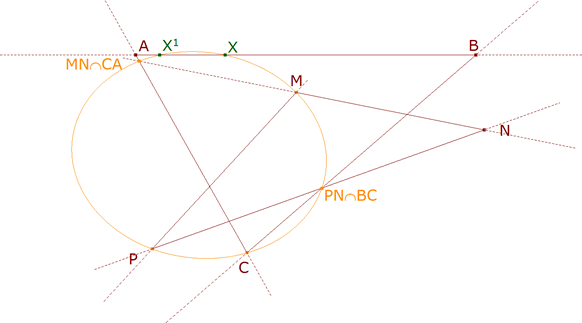
4.2 LA CÓNICA figura 5 Aplicando el TEOREMA DE CHASLES STEINER es claro que el lugar geométrico de R” es una cónica Γ; ya que R” = MR∩PR’ es la intersección de las rectas correspondientes de dos haces homográficos. Recordemos que en general no tenemos el dibujo de la cónica y que podemos bastarnos con cinco puntos. Estando atentos a la definición de h_AB, vemos que podemos prescindir del punto inicial R y sólo con el enunciado tenemos los cinco puntos: punto 1: M, por el teorema de Chasles Steiner. punto 2: P, por el teorema de Chasles Steiner. punto 3: C por la definición de h_{AB y}h_AB. punto 4: MN∩CA por la definición de h_{AB y}h_AB. punto 5: PN∩BC* por la definición de h_{AB y}h*_AB. Como sabemos resolver la intersección de la cónica Γ con la recta AB, obtenemos los puntos X,X¹ = AB∩Γ En este caso, aprovecharemos CABRI II para hacerlo y además el dibujo de la cónica hará los gráficos más amenos.

5. LA SOLUCION	Segunda solución

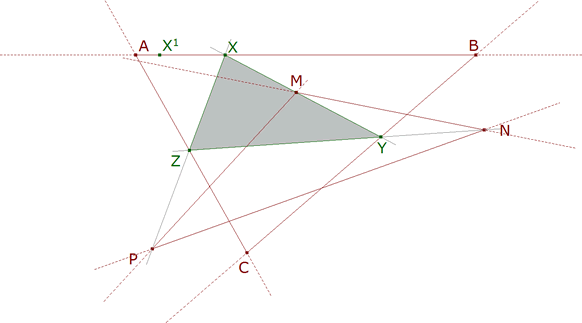
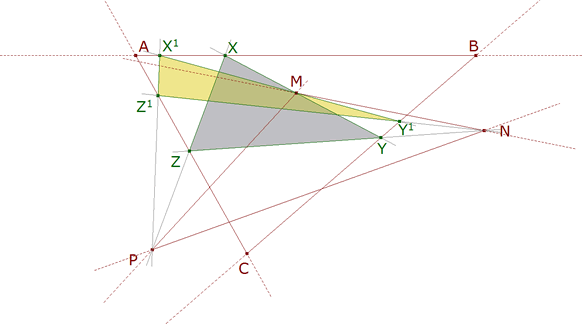
5.1 PASO A PASO figura 6 a) Dibujamos los triángulos ABC y MNP con los cinco puntos M, P, C, MN∩CA, PN∩BC. figura 7 b) Hallamos la intersección de la cónica Γ con AB. Obtenemos X, X¹ si existen. figura 8 c) MX corta a BC en Y, PX corta a CA en Z. Trazamos el triángulo XYZ. figura 9 f) MX¹ corta a BC en Y¹, PX¹ corta a CA en Z¹. Trazamos el triángulo X¹Y¹Z¹.

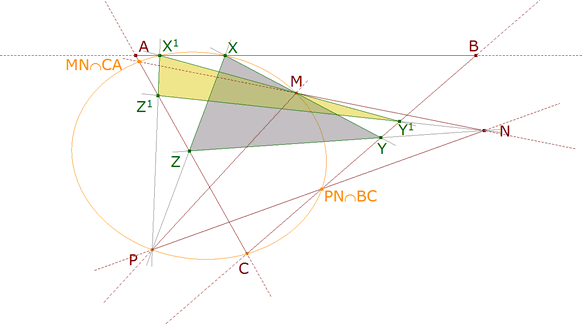
4.2 TODO JUNTO figura 10